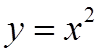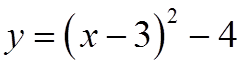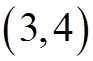SECTION 8.1 INTRODUCTIONS TONON LINEAR FUNCTIONS
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) TERMS:
Input Number: (x) Numbers that you putinto a function (Not every number ispossible)
Output Number: (y) Numbers you get out ofa function
Function: A Rule/Equation that produces asingle output number for each inputnumber

II) EXAMPLES OF FUNCTIONS:
i) Square Function:
Squares the number
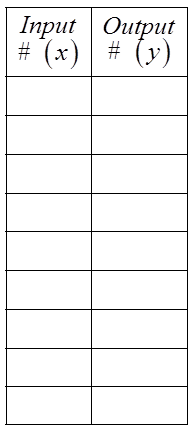
ii) Root Function
Square roots the number
Input number can not be
Negative
iii) Reciprocal Function
Takes the reciprocal ofthe number
Input number can not be zero
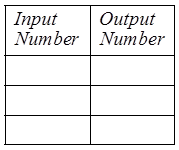
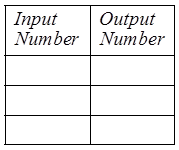
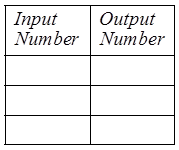
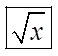
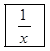

III) GRAPHING A FUNCTION
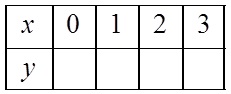
Make a T.O.V.
Each pair of Input/Output number is a pair ofcoordinates (point) for the function
Input Number (X axis), Independent Axis
Output Number (Y axis), Dependent Axis

EX: GRAPH
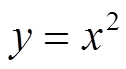
x
y
-4
-3
-2
-1
0
1
2
3
4
2
4
6
8
10
x
y
-4
-3
-2
-1
0
1
2
3
4
2
4
6
8
10

PRACTICE: GRAPH
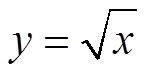

x
y
0
10
20
30
2
4
6
x
y
0
10
20
30
2
4
6

PRACTICE: GRAPH
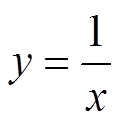

x
y
-8
-6
-4
-2
0
2
4
6
8
-8
-6
-4
-2
2
4
6
8
x
y
-8
-6
-4
-2
0
2
4
6
8
-8
-6
-4
-2
2
4
6
8

II) ABSOLUTE VALUE FUNCTION
The absolute value of any real number willbecome positive
Negative Positive
Positive Positive
Note: An absolute value function will take anypoint with a negative y-coordinate and change itto a positive y-coordinate
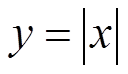
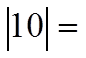
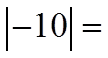
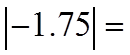

III) GRAPHS OF ABSOLUTE VALUE FUNCTIONS
The ABS function will reflect any part ofthe function under the x-axis to above thex-axis
The ABS of a straight line is a V-shape
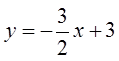
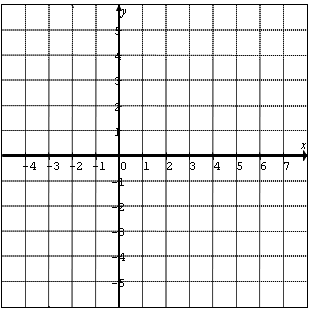
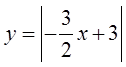
The center of the graph is atthe x-intercept
There are two sides: Left & Right

IV) HOW CERTAIN FUNCTIONS LOOK LIKE?
Linear FunctionStraight Line
Quadratic Function
U-shaped Graph
Root Function
U shaped on its Side
Reciprocal Function
Cross (2 separate Parts)
Absolute Value Function
Cross (2 separate Parts)

V) GRAPHING QF:
A Quadratic function in standard form is much easierto graph
Using constants “a”,”p”, & “q”, we can find the vertex,which way it opens and the congruency value
Vertex: Axis of Symmetry:
Domain:Range:
Y intercept: make x=0, solve for y
X-intercept: make y=0, solve for x
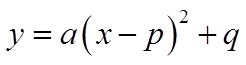
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FOR EACH OF FOLLOWING EQUATIONS, FIND THECONSTANTS “A”, “P”, “Q”, VERTEX, AND A.O.S.
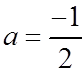
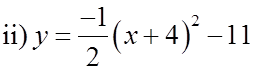
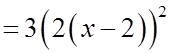
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) CONSTANTS “P” AND “Q”
The constant “p” affects the graph horizontally
When p=0, the graph is centered on the Y-axis
x
y
0
x
y
0
x
y
0
2 unitsRight
2 unitsLeft
x
y
0
x
y
0
2 unitsup
2 unitsDown
InteractiveApplet
The constant “q” affects the graph vertically
© Copyright all rights reserved to Homework depot: www.BCMath.ca




VII) HOW DOES THE CONSTANT “A” WORK?
5
5
3
3
1
1
Beginning at the vertexwe can graph all theother points withoutmaking a TOV
Each point increaseshorizontally by 1but increases verticallyby 1 , 3 , 5 , 7 , 9, …
7
7
© Copyright all rights reserved to Homework depot: www.BCMath.ca


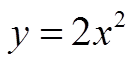
6
10
10
6
2
2
If “a = 2”, the pointsgo up faster.
Each point increaseshorizontally by 1but increases verticallyby 2 , 6 , 10 , 14 , 18, …

Simply multiply thevalues by “2”
© Copyright all rights reserved to Homework depot: www.BCMath.ca