
SECTION 4.6COMPLETING THE SQUARE

PERFECT TRINOMIALS:
When a perfect trinomial is factored, both binomials will be equal
The third term in a perfect trinomial is equal to the secondterm divided by 2 and then squared
The term in the binomial is equal to the second term dividedby 2
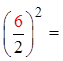
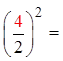
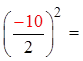
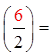
When we CTS, we change the trinomial into a perfecttrinomial
© Copyright all rights reserved to Homework depot: www.BCMath.ca

WHAT IS “COMPLETING THE SQUARE”
“Completing the Square” is a process that converts aquadratic function that can not be factored to a form thatcan be solved algebraically
Suppose we have the following trinomial
If we complete the square, we end up with the expressionon the right
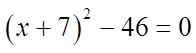
Can’t factor this…
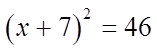
We end up with two answersin radical form

HOW TO COMPLETE THE SQUARE
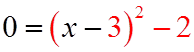
Bracket the first two terms!
Divide the second term by 2 andsquare it!Purpose: Make the expression in thebracket into a perfect square!
Take the negative square outsideof the brackets!
The trinomial becomes twoequal binomials
Now you can solve this equation bysquare rooting both sides:
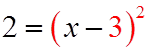

EX: COMPLETE THE SQUARE AND SOLVE FOR “X”
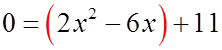
Bracket the first two terms!
Divide the second term by 2 andsquare it!
Take the negative squareoutside of the brackets andmultiply with coefficient infront!
The trinomial becomes twoequal binomials
Solve for “x” by squarerooting both sides
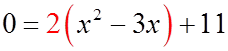
Factor out any coefficient for x2

Ex: The sum of two numbers is 80. Their product is1600. Find the numbers
GatherInformation
There are two numbers, let ‘x’ and ‘y’be the numbers
The sum is 80
The product is 1600
Substitute the first equationinto the second one.
The two numbersare 30 and 80

Ex: The difference of two numbers is 10. The sum oftheir squares is 60. Find the numbers
Gather Information
There are two numbers, let ‘x’ and ‘y’be the numbers
The difference is 10
The sum of theirsquares is 60
Substitute the first equationinto the second one.
The two sets of numbersare:

Find the vertex because:
The vertex is the minimum
1. Complete the square
The minimumoccurs when x =-5
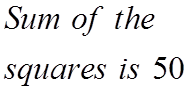

HOMEWORK: