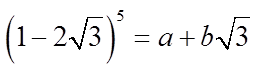SECTION 4.2EXPANDING BINOMIALS USINGPASCAL’S TRIANGLE
© Copyright all rights reserved to Homework depot: www.BCMath.ca
BLAISE PASCALE AND PASCAL’S TRIANGLE
Blaise Pascal (June 19, 1623 – August 19, 1662) was a Frenchmathematician, physicist, and religious philosopher
He used the triangle to solve problems in probability theory.
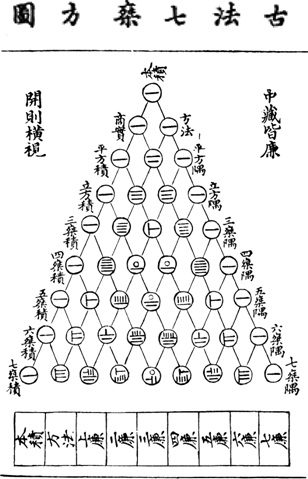
Numbers used in Pascal’s triangle was discovered by manymathematicians before him but with different applications
The earliest explicit depictions of the triangle occur in the 10thcentury in commentaries on the Chandas Shastra (India)
In Iran, it is known as "Khayyam triangle” (1048-1131); , finding nthroots of a binomial expansion (section 6.6)
In China, it is known as “Yang Hui'striangle"(1238-1298)
In Italy, they call it "Tartaglia's triangle", used insolving cubic polynomials(1500-1577)
200px-Blaise_Pascal.jpg
Yanghui_triangle.gif
PASCAL’S TRIANGLE
1
Begin with three 1’s on the top
Each number is the sum of thevalues directly above
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
1
10
45
120
210
252
210
120
45
10
1
EXPANDING BINOMIALS
Expand the following Binomials:
The coefficients of all the terms corresponds tothe numbers in Pascal’s Triangle!
© Copyright all rights reserved to Homework depot: www.BCMath.ca
BINOMIAL THEOREM:
When expanding a binomial in the form of (a+b)n, we can usePascal’s triangle to determine the coefficients of each term
Rules:
The exponent “n” to determines which row to use fromPascal’s triangle    use the “n+1” row
There will be “n+1” terms in the expansion
The first term must have a power of an, with the “a”variable descending in degree by one
In addition, the first term will have b0, with each termascending in degree by one
Note: for every nth power, there will be n+1 terms
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Ex: Expand the following binomial:
n = 4, so use the 5th rowin Pascal’s triangle
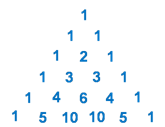
pascal's triangle 2.png
The first variable “a” will bedescending in power, starting with 4
The second variable “b” will beascending in power, starting with 0
n = 5, so use the 6th rowin Pascal’s triangle
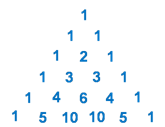
pascal's triangle 2.png
The first variable “a” will bedescending in power, starting with 4
The second variable “b” will beascending in power, starting with 0
Simplify each term!
PRACTICE: EXPAND THE FOLLOWING BINOMIALI) INDICATE HOW MANY TERMS THERE AREII) WHAT IS THE COEFFICIENT OF THE TERM WITH X3
pascal's triangle 3.png
n = 6, so there will be 7 terms in the expansion
Use the 7th row in Pascal’s Triangle
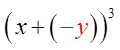
n = 3, so there will be 4 terms in the expansion
Use the 3rd row in Pascal’s Triangle
Simplify the exponents
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Coefficient of the term with x3 is 20
Coefficient of theterm with x3   is 1
EX: FIND THE CONSTANT TERM:
“the constant term” has no variables
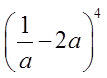
Expand the binomial
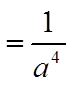
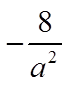
The constant term is 24
EX: SOLVE FOR “A” AND “B”