SECTION 4.3 SOLVING PROBLEMSAND EQUATIONS WITH POLYNOMIALFUNCTIONS

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) SOLVING POLYNOMIAL FUNCTIONS:

Ex: Given the following equation, solve for “x”

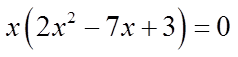
Factor the polynomial

Factor the trinomial

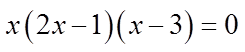
Solve for “x” from eachbracket

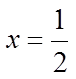
Factor the polynomial using thefactor theorem

Solve for “x” from each bracket

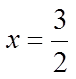
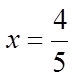
EX: DETERMINE THE EQUATION OF A FUNCTION WITHROOTS: -1, 1, 3 AND Y-INTERCEPT OF -6.

Plug the roots into the equation in factored form

Plug the coordinates of the point into the equation tosolve for “a”

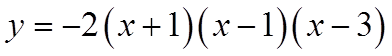
II) CUBIC FUNCTIONS AND CARDBOARD BOXES

Every year, millions of cardboard boxes are made

Multi-million dollar business

One of the most effective ways oftransporting cargo

BOX ACTIVITY

A box is made from a flat rectangular sheet of cardboard

Cut out 4 squares from each corner to make a box

Goal: Maximize the volume of the box

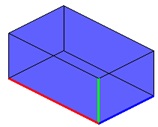
Flat Piece ofCardboard

Cut out four squaresfrom each corner

Fold along the bluelines to make a box

The middlerectangle is thebase of the box

BASE

The length of thebox is now:L - 2x

The  width of thebox is now:W - 2x

The  height ofthe box is :  x

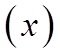
EX: A PIECE OF CARDBOARD THAT IS 30CM X 20CM ISCUT/FOLDED INTO A BOX.  DETERMINE THE DIMENSIONS THATWILL MAXIMIZE THE VOLUME OF THE BOX.

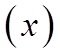
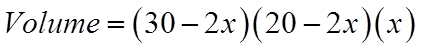
“x” is the height of the box

The height must be smaller than the length andwidth of the box.

Graph the equation:

To find the Maximum Volume, look for arelative Maximum!

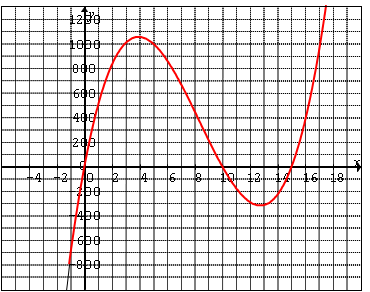
Graph the equationwith Ti-83

Change the window:

Xmin: -10        Xmax: 25

Ymin: -1000    Ymax:1500

Find the Relative Max

For the Maximum Volume:

X=3.923

Y=1056.3

The maximum volume is                      when you cut outsquares with side lengths of 3.923cm.

III) COEFFICIENTS OF A POLYNOMIAL

The coefficients of a polynomial can be used todetermine the sum and product of the roots

Suppose we have a quadratic function with two roots

Expand and FOIL

The constant “C” isequal to the productof the roots

The coefficient “B” isthe negative sum ofthe roots

Negative product of all the roots

Negative sum of all the roots

Challenge: Given that the roots of the polynomial below are“a”, “b” and “c”, find the following:

i) Find the value of

Gather information

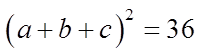
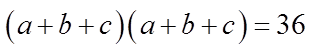
HOMEWORK: ASSIGNMENT 4.3