SECTION 4.2FACTORING POLYNOMIALFUNCTIONS

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) REMAINDER THEOREM:

When a polynomial,          , is divided by a binomialthe remainder will be the number you get fromsubstituting “k” into

is the remainder when

is divided by

Ex: Find the remainder:

Make the dividend equal to f(x)

Use the divisor to find “k”

The remainder is the Y-coordinate!!

PRACTICE: FIND THE REMAINDER USING THE REMAINDERTHEOREM:

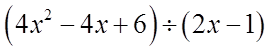
Make the dividend equal to f(x)

Use the divisor to find “k”

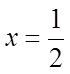
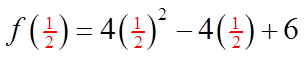
II) FINDING A MISSING CONSTANT USING THEREMAINDER THEOREM:

Ex: When the equation:                                is divided by

                then remainder is 1.  What is the value of “m”?

Make the dividend equal to f(x)

Use the divisor to find “k”

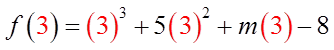
Plug in the remainderand solve for “m”

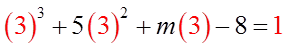
PRACTICE: WHEN THE EQUATION:IS DIVIDED BY (3X+1) THE REMAINDER IS 11. FIND M

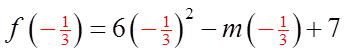
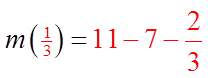
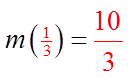
One learning outcome in this section is to convert afunction from “General Form” to “Factor Form”

We can use the Remainder thm to find the first factor(Remainder is zero)

Divide the polynomial by the 1st factor to find the quotient

Factor the quotient until you can’t factor anymore

An equation in factored form can be solved easily

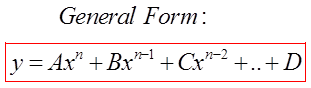
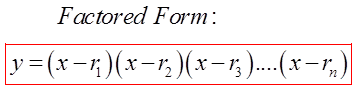
III) CONVERTING TO GENERAL FORM:

PRACTICE: INDICATE THE ROOTS FROM THE FOLLOWINGGRAPH

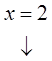
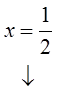
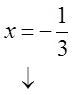
The roots are:

x

y

-1

0

1

2

-7

-6

-5

-4

-3

-2

-1

1

2

3

4

5

Each root is a x-intercept.

When you know thex-intercepts, you caneasily write the equationin factored form.

To find the constant“a” plug in thecoordinates of aknown point

PRACTICE: GIVEN THE GRAPH, FIND THE ROOTS,FACTORS, AND EQUATION IN FACTOR FORM:

x

y

-5

-4

-3

-2

-1

0

1

2

3

4

5

-10

-8

-6

-4

-2

2

4

6

8

10

x

y

-3

-2

-1

0

1

2

-4

-2

2

4

6

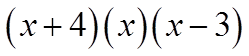
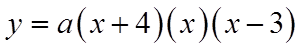
IV) FACTOR THEOREM:

When you divide a polynomial function, f(x), by any oneof its factors, the remainder will be zero

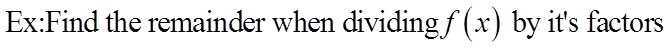
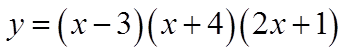
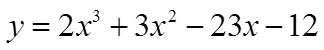
Remainder is zero

The factors are:

Use Remainder Theorem:

EX: WHICH OF THE FOLLOWING IS A FACTOR OF F(X)

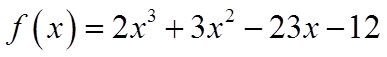
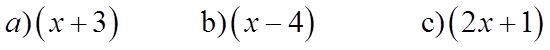
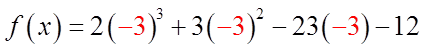
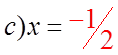
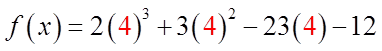
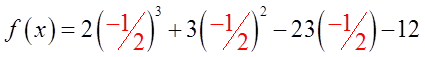
III) STEPS FOR BREAKING DOWN A POLYNOMIALFUNCTION FROM GENERAL TO FACTORED FORM:

Find your first “Root” or “Factor”

Remainder theorem

TOV   on   Ti-83

Your roots are usually numbers that multiply tothe constant term in the dividend

Find the Quotient

Dividing f(x) by its factor (x-r)

Long Division or Synthetic Division

The remainder must be zero

Factor the Quotient

BUM Method, Criss-Cross Method

Split the quotient (trinomial) to two binomials

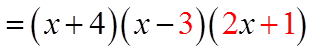
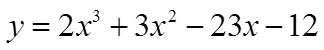
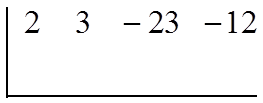
Find the Quotient

Find the First Root: Rem. Thm.

Synthetic Division

EX: CONVERT THE FUNCTION TO FACTOR FORM:

Start with numbers thatmultiply to the constant term

NOT every number works!

Factor the Quotient

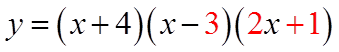
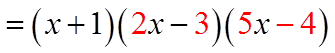
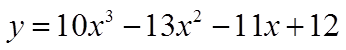
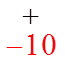
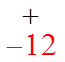
Find the Quotient

Find the First Root: Rem. Thm.

Synthetic Division

EX: CONVERT THE FUNCTION TO FACTOR FORM:

Start with numbers thatmultiply to the constant term

Factor the Quotient

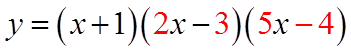
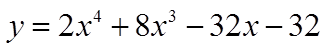
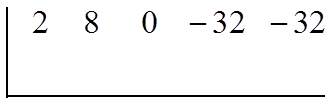
Find the Quotient

Find the First Root: Rem. Thm.

Synthetic Division

CHALLENGE: CONVERT THE FUNCTION TO FACTOR FORM:

Start with numbers thatmultiply to the constant term

The Quotient needs to befactored again

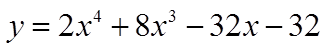
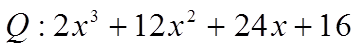
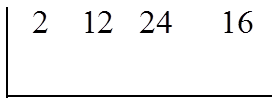
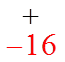
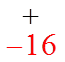
Find the Quotient

Start Over and Find the FirstFactor for the Quotient

Synthetic Division

CHALLENGE: CONVERT THE FUNCTION TO FACTOR FORM:

Use the Remainder Theorem

Factor the Quotient

HOMEWORK: ASSIGNMENT 4.2