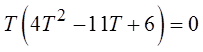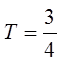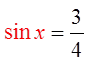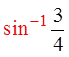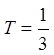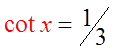SECTION 3.8 SOLVINGTRIGONOMETRIC EQUATIONSAND HC
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) REVIEW: SOLVING
“Solving” means finding a value for the variable, so thatboth sides of an equation will be equal
There are several ways to solve a Trigonometric equation:
Algebraically: (Ch5.2)
Isolate the variable using BEDMAS
Use inverse trig. functions to find the solution(s)
There are usually two solutions within one cycle (CAST)
Use the reference angles to find the solution in standard position
Graphically:
Make Y1 equal to one side of the function
Make Y2 equal to the other side
Then find the points of intersection(s)
Points where the graph intersect the x-coordinates are thesolutions
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: SOLVE THE EQUATION FOR 0 ≤ Θ ≤ 3Π
Make the left side of the equation y1
Make the right side of the equation y2
Solve the system by findingthe points of intersection
Press:
2nd
TRACE
#5: Intersect
1st Curve?
ENTER
2nd Curve?
ENTER
Guess?
ENTER
Repeat this process untilyou find all the points ofintersection
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: SOLVE THE EQUATION FOR 0 ≤ X ≤ 2Π
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) FINDING THE GENERAL SOLUTION:
When finding the general solution, only one pair of solutions within acycle is needed
Other solutions can be founded by adding/subtracting multiples ofthe period (Co-terminal angles)
Graphically, the horizontal distance between 2 solutions in separatecycles is equal to the period
The two general solutions will be:
If you want to find solutionswithin other cycles, then justadd/subtract the period
© Copyright all rights reserved to Homework depot: www.BCMath.ca

























x
y
-1
1
III) SOLVING TRIGONOMETRIC FUNCTIONS WITHHORIZONTAL COMPRESSIONS:
Ex: Find the value of θ, for 0 ≤ θ ≤ 360°
The sine function is compressed horizontally by a factor of 3
The number of solutions will increase from 2 to 6 solutions between 0° and 360°
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN THE FOLLOWING SYSTEM, HOW MANYSOLUTIONS WILL THERE BE BETWEEN 0 ≤ Θ ≤ 360° ,WHERE “B” IS A CONSTANT
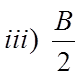
The constant “B” will indicate the horizontal factor ofexpansion/compression
If B=2, then the graph will compress horizontally bya factor of ½. There will be 2 cycles between 0 & 360°
If B=3, then the graph will compress horizontally bya factor of 1/3. There will be 3 cycles between 0 & 360°
The number of solutions will be 2 x B
































x
y
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
-1
1
































x
y
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
-1
1


© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) SOLVING TRIGONOMETRIC EQUATIONS ALGEBRAICALLY
Isolate the variable using BEDMAS
Use inverse trig. functions to find the solution(s)
There are usually two solutions within one cycle (CAST)
Use the reference angles to find the solution in standardposition
When there is a horizontal compression, add the period tofind other sets of solutions
© Copyright all rights reserved to Homework depot: www.BCMath.ca

V) SOLVING EQUATIONS WITH HORIZONTAL COMPRESSIONS
Make the substitution: 3x = θ
Ex: Solve for “x”, 0 ≤ x ≤ 2π
Isolate the trigonometric Function
Solve for θ in Quadrant 2
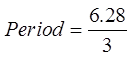
Add the period to find solutions in the next cycle
To Solve for “x”, substitute 3x back into θ
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: SOLVE FOR “X”, 0 ≤ X ≤ 2Π
Make the substitution: 2x = θ
Isolate the trigonometric Function
Solve for θ in Quadrant 4
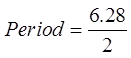
Add the period to find solutions in the next cycle
To Solve for “x”, substitute 2x back into θ
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) SOLVING TRIGONOMETRIC EQUATIONS USING ALGEBRA
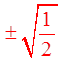
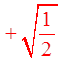
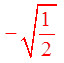
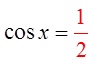
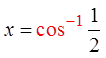
Ex: Solve for “x”, 0 ≤ x ≤ 2π
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Factor


VII) SOLVING TRIGONOMETRIC EQUATIONS INVOLVING SUBSTITUTION
Make the substitution: sin x = T
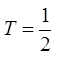
Substitute T back into sin x
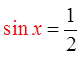
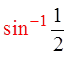
Ex: Solve for “x”, 0 ≤ x ≤ 2π
© Copyright all rights reserved to Homework depot: www.BCMath.ca


VIII) USING DOUBLE ANGLE IDENTITIES TO SOLVE EQUATIONS
Ex: Solve the following equation for 0 ≤ θ ≤ 360°
Note: You are “Solving for θ”,not proving an identity!!
Use the Double-Angle Identity
Factor the equation
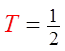
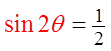
Solve for θ from each equation.
Remember to use CAST and there
are TWO cycles between 0 and 360°
Add the period (180°) to find other solutions
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: SOLVE FOR 0 ≤ Θ ≤ 360°
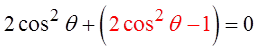
Use the Double-Angle Identity
Factor: Difference of Square
Solve for θ from each equation.
Remember to use CAST
Note: There is only ONE cycle
Between 0 and 360°
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Make the substitution:
tan(2x) = T
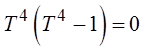
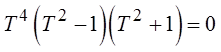
Challenge: Solve for “x”, 0 ≤ x ≤ 2π
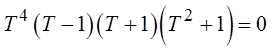
Add the period to findsolutions in the next cycle
© Copyright all rights reserved to Homework depot: www.BCMath.ca


HOMEWORK
Assignment 3.8