
SECTION 3.6 BASICTRIGONOMETRIC IDENTITIES
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) WHAT IS A TRIGONOMETRIC IDENTITY?
A trigonometric identity is an equation that is equal for allvalues of the variable(s) for which the equation is defined
Examples of trigonometric identities
Trigonometric equations that are not Identities
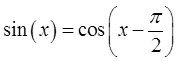
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Equation is true only at certain values of “x”
Both sides are equal for all values of “x”
Graphically, if both sides overlap each othercompletely, then the equation is an identity
Graphically, both sides only intersect at certainpoints, then the equation is NOT an identity

II) ODD VS EVEN IDENTITIES:
Even Identities: An function that looks the same when reflectedover the y-axis (Horizontal Reflection)
Odd Identities: A function that looks the same when reflectedover both the X and Y axis
























x
y
-1
1
























x
y
-1
1
© Copyright all rights reserved to Homework depot: www.BCMath.ca

III) PYTHAGOREAN IDENTITIES:
Review: The coordinates of any point on the circumference of anunit circle can be represented by:


X-coordinate
Y-coordinate
Since:
PythagoreanIdentity
Other Pythagorean Identities can be generated by dividing allterms by either “cos2x” or “sin2x”
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) BASIC IDENTITIES
Odd- Even Identities
Reciprocal Identities
Quotient Identities
Pythagorean Identities
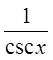
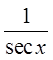
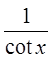
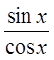
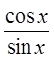
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Other identities can be created by manipulating the equation

V) VERIFYING AND PROVING IDENTITIES
There are two ways to Verify an identity
Plug variety of numbers into the equation
If the equation is equal for all the values, then theequation is an identity OR
Graph the equations, if they completely overlap, then it’san identity
Proving an Identity
Simplify the equation algebraically and then show thatboth sides are equal
When proving algebraically, first convert all functionsinto sine or cosine
Then simplify using basic identities
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: VERIFY THE FOLLOWING IDENTITY:
NUMERICALLY:
GRAPHICALLY:
Pick a random number
Both sides are equal!
Pick another number
Both sides are equal again!
























x
y
-4
-3
-2
-1
0
1
2
3
4
-2
-1
1
2
Since the graphsoverlap each other
completely, then it
must be an identity
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Since the equation is equal for bothverifications, then it’s likely to be anidentity

PRACTICE: VERIFY THE FOLLOWING IDENTITIES NUMERICALLY:
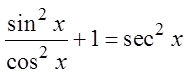
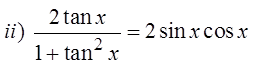
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Pick a random number for “x”
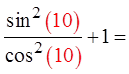
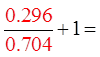
Try another value for “x”
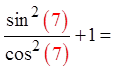
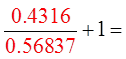
Both sidesare equal
Since the equation is equal forboth verifications, then it is likely to be an identity
Make “x” = 10 rad.
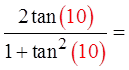
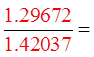
Make “x” = 2 rad.
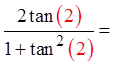
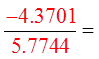
Both sidesare equal
The equation is likely to
be an identity

PRACTICE: VERIFY EACH OF THE FOLLOWING IDENTITIES:
Numerically:
Graphically:
© Copyright all rights reserved to Homework depot: www.BCMath.ca
























x
y
-2
-1
1
2
Numerically:
Graphically:
Not an Identity!!
























x
y
-2
-1
1
2

VI) PROVING IDENTITIES ALGEBRAICALLY:
When proving trigonometric identities:
Convert all trig. functions to sine or cosine
Use basic trig. Identities to simplify complicated ones
Odd/Even, Quotient, Pythagorean Identities
Start with the side that looks “more complicated”
You may need to rationalize the expression, factor outcommon factors, or multiply all terms by the LCD
Trial and Error (Do whatever it takes)
Once the left side and right side are equal then theequation is a trigonometric identity
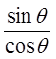
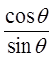
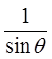
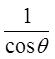
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VII) PROVING TRIGONOMETRIC IDENTITIES BY USING BASICIDENTITIES:
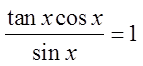
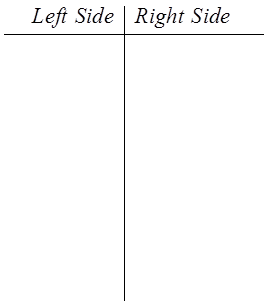
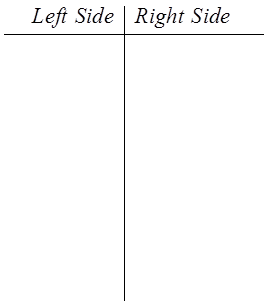
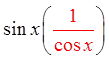
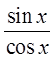
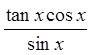
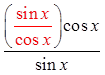
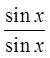
Quotient Identity!
Since the left side looks morecomplicated, we will prove theidentity from the left
Cancel out commonfactors
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VIII) PROVING BY ADDING/SUBTRACTING IDENTITIES
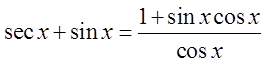
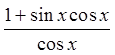
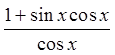
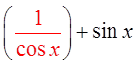
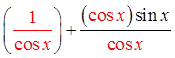
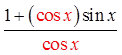
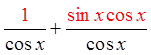
The proof may be the different
but the result is the same
You can also prove the identityfrom the other side
CommonDenominator
Combine the
Fractions
Split into 2separatefractions
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: PROVE THE FOLLOWING IDENTITIES:
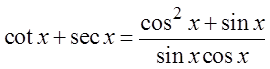
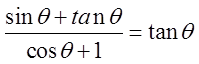
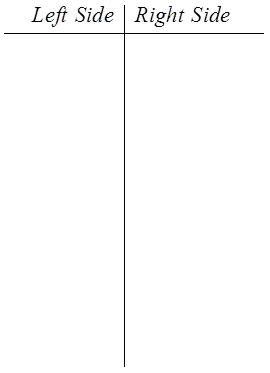
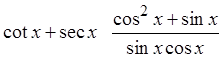
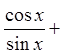
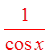
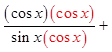
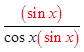
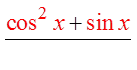
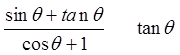
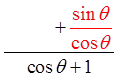
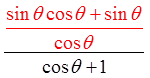
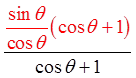
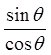
Factor out sin θ
CommonDenominator
Combine the
Fractions
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Get the LCD withthe numerator
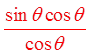

IX) PROVING IDENTITIES USING FRACTIONS :
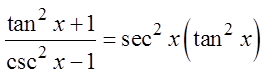
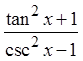
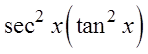
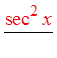
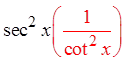
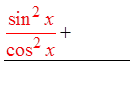
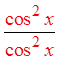
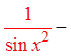
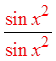
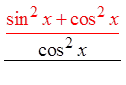
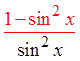
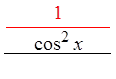
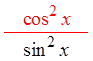
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Pythagorean
Identities
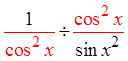
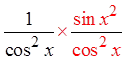
Divide thefractions

X) PROVING IDENTITIES BY FACTORING:
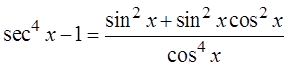
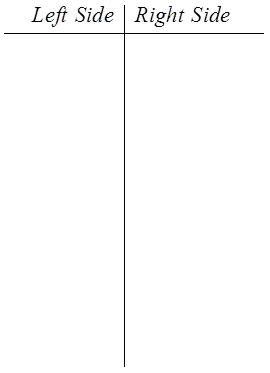
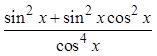
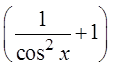
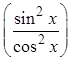
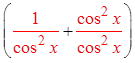
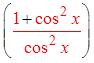
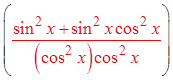
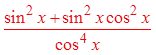
Difference ofsquares
Pythagoreanidentity
CommonDenominator
Expand
Factor out thesine function
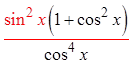
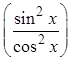
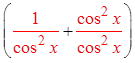
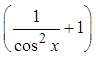
© Copyright all rights reserved to Homework depot: www.BCMath.ca
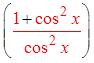
PythagoreanIdentity
FOIL

PRACTICE: PROVE THE FOLLOWING IDENTITIES BY FACTORING
Bracket thelast 2 terms
Pythagoreanidentity
Factor: Difference
of squares
PythagoreanIdentity
Factor theTrinomial
© Copyright all rights reserved to Homework depot: www.BCMath.ca

XI) PROVE BY CONJUGATING THE EXPRESSION:
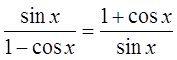
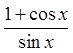
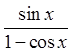
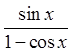
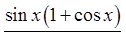
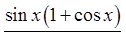
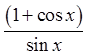
Multiply both top &bottom by the conjugate
Pythagoreanidentity
Expand
Quotient Identities
Reciprocal Identity
Pythagorean Identity
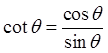
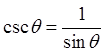
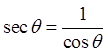
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Formula Sheet

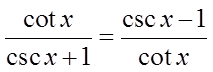
PRACTICE: PROVE THE FOLLOWING IDENTITY BY CONJUGATINGTHE EXPRESSION:
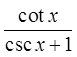
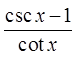
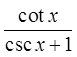
Multiply both top &bottom by the conjugate
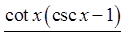
Expand
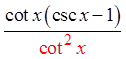
Pythagoreanidentity
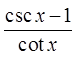
Quotient Identities
Reciprocal Identity
Pythagorean Identity
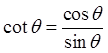
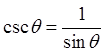
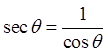
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Formula Sheet
CLOSE

HOMEWORK:
Assignment 3.6