
SECTION 3.3 GRAPHING SINECOSINE AND TANGENTFUNCTIONS
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) WHAT IS A PERIODIC FUNCTION?
A function that repeats its output values in a cycle
The range of input values within a cycle is known as theperiod
There are many examples of periodic functions in ourworld
Ocean waves and ocean currents
Solar system
Finance and Market trends
Sound waves, light transmission, radiation
Wave propagation: earthquakes,
Heart beat
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) COMPONENTS OF A PERIODIC FUNCTION:
x
y
Crest
Trough
Period
Crest: Local maximums on the periodic function. Top
Trough: Local minimums on the periodic function. Bottom
Amplitude: The vertical difference between the top and the middle
Period: The horizontal difference between two rests or two troughs
Note: The horizontal distance between the crest and trough is HALF the
period.


Amplitude
Period

½ of Period
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given each graph, indicate the period and amplitude






































x
y
-3
-2
-1
0
1
2
-4
-3
-2
-1
1
2
3
4






































x
y
-3
-2
-1
0
1
2
-4
-3
-2
-1
1
2
3
4


Period
Amplitude
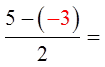


Period
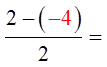
Amplitude
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: If high tide occurred at 7:30am and low tide was at1:30pm, what time will the next high tide be?
The time difference between high tide and low tide is half the period
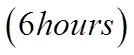
The time for a full period will be 12 hours
So the next high tide will be 12 hours from 7:30am
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HIGH AND LOW TIDE:

At high tide, the ocean levels go up
At low tide, the ocean levels go down
Ocean levels will fluctuate
up and down over several hours

III) SINE FUNCTION IN AN UNIT CIRCLES:
Sinθ in an unit circle is equal to the y-coordinate of point “P”
The highest y-coordinate is at 1 (at 90°) & the lowest at -1 (at 270°)
The value of Sinθ changes periodically from 1 to -1 depending onthe value of the angle
If we graph the sine function, we are comparing how height of pointP changes in relation to the angle in standard position

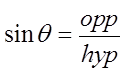
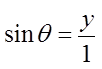
Y-coordinate
Note: hyp= 1
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) GRAPHING THE SINE FUNCTION:
X-axis: value of the central angle in radians
Y-axis: value of sinθ, height of point “P”
Highest (1) and lowest (-1)










































x
y
-0.5
0.5
-1
1
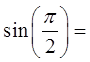
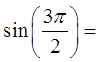
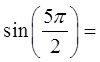
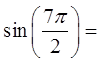
© Copyright all rights reserved to Homework depot: www.BCMath.ca

SINE FUNCTION:
























x
y
-1
-0.5
0.5
1

As you rotate the terminal arm, the value of the angleincreases
The height of the graph changes fluctuates up anddown in accordance to the angle
The result is a wave function
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Find the following for the sine function:
a)Period & amplitude
b)Y intercept
c)X intercept and a general formula
d)Domain and Range










































x
y
-0.5
0.5
Period
Period:
Amplitude


Amplitude
X-intercepts:
Y-intercepts:
Domain:
Range:

V) COSINE FUNCTION IN AN UNIT CIRCLES:
Cosθ in an unit circle is equal to the x-coordinate of point “P”
The lowest x-coordinate is -1 (at 180°) & the highest is 1 (at 360°)
The value of Cosθ changes periodically from 1 to -1 depending onthe value of the angle
If we graph the Cosine function, we are comparing the horizontaldistance of point P vs the angle in standard position

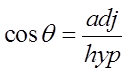
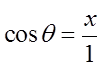
x-coordinate
Note: hyp= 1
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) GRAPHING THE COSINE FUNCTION:
X-axis: value of the central angle in radians
Y-axis: value of cosθ, x-coordinate point “P”
Highest (1) and lowest (-1)










































x
y
-0.5
0.5
-1
1
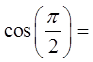
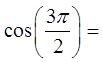
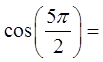
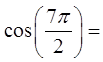
© Copyright all rights reserved to Homework depot: www.BCMath.ca

COSINE FUNCTION:
























x
y
-1
-0.5
0.5
1

Rotate your unit circle, so you can measure the horizontaldistance of point P
The Cosine graph will then begin at the top
Then you graph how the horizontal distance of P changesin relation to the angle in standard position
The result is a wave function
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Find the following for the cosine function:
a)Period & amplitude
b)Y intercept
c)X intercept and a general formula
d)Domain and Range










































x
y
-0.5
0.5
Period
Period:
Amplitude


Amplitude
X-intercepts:
Y-intercepts:
Domain:
Range:

VII) SUMMARY FOR GRAPHING COSINE/SINE FUNCTIONS
When graphing a Sine & Cosine function, there are only 5points to consider: Beginning, Middle, End, Quarter way,and 3 Quarters way of the period
Sine Function:
At the Beginning, Middle, and End of the period, thewave will cross the x-axis
At quarter way, the graph will be at the top
At 3-quarters way, the graph will be the bottom
Cosine Function
At the Beginning and End of the period, the graph will beat the top
In the Middle, the wave will be at the bottom
At quarter way & 3 quarters way, the graph will be on thex-axis
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: What is the equation for the following graph?










































x
y
-0.5
0.5
The graph is a sine function with avertical reflection

REVIEW: TANGENT FUNCTION & TANGENT LINES
SOH-CAH-TOA
Using the ratio of opposite over adjacent, we can showthat the tangent function is also sine over cosine
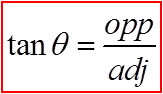
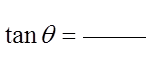
A tangent line is a line that crosses a circle at onlyone point
Tangent Line
Point of Tangency
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VIII) TANGENT FUNCTIONS AND UNIT CIRCLES
There are two ways to relate the tangent function with anunit circle
1st Method
The tangent function can be defined as the y-coordinate ofPoint P, divided by its x-coordinate
2nd Method
The tangent function can be defined as the y-coordinate ofthe extension of the terminal arm on a vertical tangent line
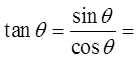
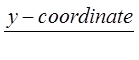
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IX) TANGENT = Y-COORDINATE / X-COORDINATE
The tangent function is the ratio of the Y-coordinateover the X-coordinate
As we rotate the around the unit circle, the ratiochanges according to the angle in standard position
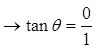
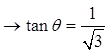
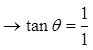
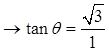
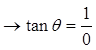
© Copyright all rights reserved to Homework depot: www.BCMath.ca

X) TANGENT AS THE Y-COORDINATE ON THE VERTICALTANGENT LINE
The tangent function can be defined as the y-coordinate of theextension of the terminal arm on a vertical tangent line
When you rotate the terminal arm,the extension creates a righttriangle with a base of 1
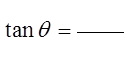
The tangent function will be theY-coordinate of this point on theVertical tangent
© Copyright all rights reserved to Homework depot: www.BCMath.ca

As the terminal arm rotates around the circle, it will cross thetangent line above the X-axis (+’ve) or below the X-axis (–’ve )
Ie: when the terminal arm is in Q1, it crosses the tangent lineabove the X-axis, so tanθ is positive
In Q2, the terminal armextends to the tangent linebeneath the X-axis, so itwill be negative
In Q3, it crosses thetangent line above the X-axis, so tanθ is positive
In Q4, it crosses thetangent line under the X-axis, so tan θ is negative
At any point when theterminal arm is pointingside ways, the value of tanθis equal to zero
At any point when it’spointing up or down, thevalue of tanθ is undefined,because it doesn’t touch thetangent line
© Copyright all rights reserved to Homework depot: www.BCMath.ca

XI) TANGENT FUNCTION AS A RECIPROCAL
The Tangent function is like a reciprocal function
At points where cosθ = 0, you will get a vertical asymptotebecause the reciprocal of zero Undefined
At points where sinθ = 0, you will be a x-intercept
At points where sinθ = cosθ , the value of tanθ will beequal to 1 (ie: 45°, 135°, 225°, and 315°, reference angleequals 45°)
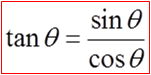
© Copyright all rights reserved to Homework depot: www.BCMath.ca









































x
y
-3
-2
-1
1
2
3
TANGENT FUNCTION
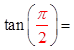
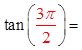
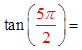
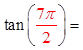




© Copyright all rights reserved to Homework depot: www.BCMath.ca



























































x
y
-2
2




The tangent function can be defined as the y-coordinate ofthe extension of the terminal arm on a vertical tangent line
As the angle changes and increase, the value of tanθ willfluctuate from negative to positive infinity
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Indicate the following for the tangent function:
a)Domain & Range
b)X-intercepts and the general formula
c)Period and amplitude








































x
y
-3
-2
-1
1
2
3




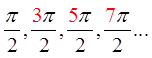
© Copyright all rights reserved to Homework depot: www.BCMath.ca

XII) VERTICAL ASYMPTOTE AND GENERAL FORMULA:
Since tanθ = (sinθ/cosθ), the vertical asymptotes will allappear when cosθ=0 (Denominator is equal to zero)
The general formula for all the vertical asymptotes in atangent function will be:
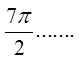
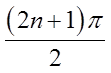
© Copyright all rights reserved to Homework depot: www.BCMath.ca
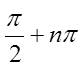

Ex: Given that 0< θ< 2π , tanθ > 0 and sinθ < 0, whatquadrant is the angle in?
If tanθ > 0 (positive), then it can only be in quadrants 1 and 3
If sinθ < 0 (negative), then it can only be in quadrants 2 and 3
To satisfy both conditions, then the angle must be in quadrant 3
© Copyright all rights reserved to Homework depot: www.BCMath.ca
