
SECTION 3.2 UNIT CIRCLES WITHSINE AND COSINE
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) REVIEW:
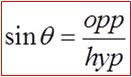
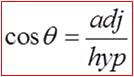
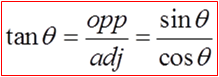
SOH-CAH-TOA
Pythagorean Theorem:
Circle Equation:
Note: The coordinate of
any point on the circumference
will satisfy the circle equation
Ratio
Function
© Copyright all rights reserved to Homework depot: www.BCMath.ca

REVIEW: SPECIAL TRIANGLES
There are two types of special triangles:
30°, 60°, 90° triangle (Equilateral Triangle) and
45°, 45°, 90° triangle (Isosceles-Right Triangle)
Cut it in half

Equilateral Triangle
All sides and angles are equal
Use Pythagorean Thm. to findthe hypotenuse of the triangle
Isosceles-Right Triangle
Two sides are equal and one angle
Is equal to 90°
Use Pythagorean Thm. to findthe height of the triangle
Isoceles 2 equal angles
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Special triangles can be used to find the exact value of sine/cosine/tangent of basic angles like: 30°, 45°, 60°, and 90°

Rather than obtaining a decimalrepresentation, we get the exact value as a fraction using special triangles
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Use the special triangles to determine the exact valuefor each of the following:
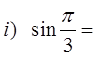
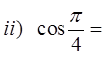
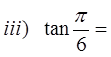

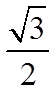
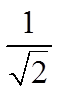
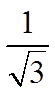
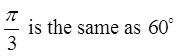
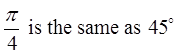
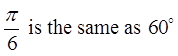
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) UNIT CIRCLES:
In a unit circle, the radius (terminal arm) is 1 unit long
The tip of the terminal arm is given by the coordinates (x,y)
the terminal arm can be used to make a right triangle, so thesum of both the “x” & “y” coordinates squared will be equal to 1


Using the Pythagorean Thm:
Any point on the circumference of a unit circle will satisfy the equation!
© Copyright all rights reserved to Homework depot: www.BCMath.ca

III) SINE & COSINE IN UNIT CIRCLES:
When given the angle in std. position, we can find the coordinates of any point on the circumferenceusing trigonometry

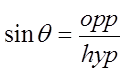
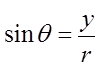
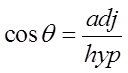
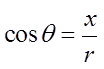
The coordinates of any point on the circumference of aunit circle can be represented by:

Y-coordinate
X-coordinate
Note: r = 1
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given the angle in standard position in a unit circle, findthe coordinates of each of the following points P(x,y).
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) SINE/COSINE/TANGENT IN DIFFERENT QUADRANTS
The sine/cosine/tangent of angles in each of the four quadrants willeither be positive or negative
Use the reference angle to determine whether if the ratio is either +’veor –’ve

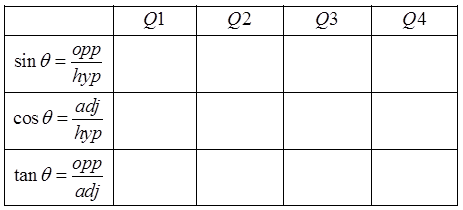





sin/cos/tan of all angles in the 1st Quadrant will be positive
Only sine of angles in the 2nd Quadrant will be positive
Cosine & Tangent in the 2nd Quad will be negative
Only Tangent of angles in the 3rd Quadrant will be positive
Sine & Cosine in the 3rd Quad will be negative
Only Cosine of angles in the 4th Quadrant will be positive
Sine & Tangent in the 4th Quad will be negative
A
S
T
C
© Copyright all rights reserved to Homework depot: www.BCMath.ca

The previous table can be used to determine whichquadrant an angle will be in when given the ratio of a trigfunction
Ex: Given each of the following trig. functions and its ratios,determine which quadrants the angle can be in:
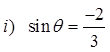
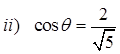
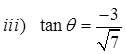
A
S
T
C
A
S
T
C
A
S
T
C
The ratio is negative
The ratio is positive
The ratio is negative
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Solve for the angle, given the following trig functions.
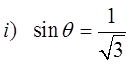
The ratio is positive
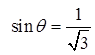
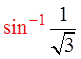
The angle has tobe in Q1 and Q2
A
S
T
C
Inverse sine the
equation to find
where the angle is
Find the 2nd angle in Q2 using
the reference angle
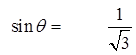
Note: When given a trig equation, there
are usually 2 answers
Check:
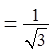
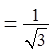
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Practice: Solve for the angle:
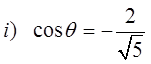
The ratio is negative
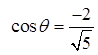
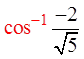
The angle has tobe in Q2 and Q3
A
S
T
C
Inverse cosine the
equation to find
where the angle is
Find the 2nd angle in Q3 using
the reference angle
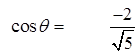
Note: When given a trig equation, there
are usually 2 answers
Check:
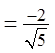
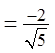
© Copyright all rights reserved to Homework depot: www.BCMath.ca

V) USING SPECIAL TRIANGLES TO SOLVE TRIG EQUATIONS
For angles with reference angles of 30°, 45°, 60°, we can usespecial triangles
Draw the angle in standard position
Find the reference angle
Draw the 30°, 60°, 90° triangle

© Copyright all rights reserved to Homework depot: www.BCMath.ca

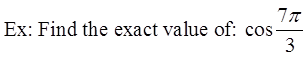
Draw the angle in standard position
Find the reference angle
Draw the 30°, 60°, 90° triangle

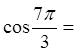
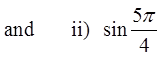
Draw the angle in standard position
Find the reference angle
Draw the 45°, 45°, 90° triangle
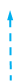

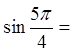
© Copyright all rights reserved to Homework depot: www.BCMath.ca

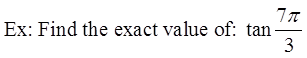
Draw the angle in standard position
Find the reference angle
Draw the 30°, 60°, 90° triangle

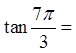
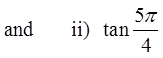
Draw the angle in standard position
Find the reference angle
Draw the 45°, 45°, 90° triangle

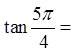
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) FINDING THE COORDINATES OF POINT P ON THETERMINAL ARM
When given the ratio of a trig function, you will be asked to findthe coordinates of the endpoint on the terminal arm
Method #1) Find the value of the central angle
Using central angle, we can find the coordinates of point P byusing:
Note: There are usually two central angles, use reference angles
Method #2) Finding the exact value using the Pythagorean Thm.
Create a right triangle in the corresponding quadrants
Use the ratios of the sides to find sinθ and cosθ
Section 3.5
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given that cos θ = 3/5 find all the possible coordinatesfor point P(x,y) in the unit circle
Determine which quadrant θ will be in
The ratiois positive
A
S
T
C



Find the coordinates using sine & cosine
The possible coordinates for P are:
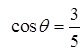
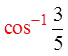
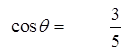
Find the angles
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Practice: Given that show the angle in standardposition, and the coordinates of P on the unit circle.
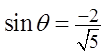
Determine which quadrant θ will be in
The ratiois negative
A
S
T
C



Find the coordinates using sine & cosine
The possible coordinates for P are:
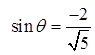
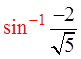
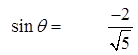
Find the angles

© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given that sin θ = and find the exactvalue of the coordinates of point P(x,y) in the unit circle
Determine which quadrant θ will be in
The ratiois negative
A
S
T
C
Use the ratio to draw a right triangle
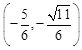

Find Base (Pythagorus)
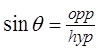
Find the coordinates using sine & cosine
Coordinates of P:
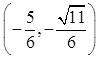
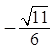
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given that tan θ = 3/5 find all the possible coordinatesfor point P(x,y) in the unit circle
Determine which quadrant θ will be in
The ratiois positive
A
S
T
C



Find the coordinates using sine & cosine
The possible coordinates for P are:
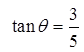
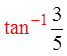
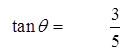
Find the angles
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:
Assignment 3.2