
SECTION 3.1 RADIANS ANDANGLES IN STANDARD POSITION
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) MEASURING ANGLES IN DEGREES
When working with angles of rotation:
Counter clockwise: Positive Angle
Clockwise: Negative Angle
Begin on the right side at zero degrees
Quarter Circle:
Half Circle:
3 Quarters Circle
Full Circle:
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca

II) CIRCUMFERENCE & RADIANS:
The circumference of a circle is given by the equation:
The radian is a unit for angle measurement
Based on measuring the arc length of a circle
1 radian is equal to an angle created by an arc length of oneradii
The arc length is equal to 1 radius
This angle will be equal to 1 radian
1 Radian
1 Radian
1 Radian
1 Radian
1 Radian
1 Radian
0.28319… Radian
A full circle will have:
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca

III) CONVERTING DEGREES TO RADIANS:
Angles in degrees will correspond with a value in radians
Radians can be written as a fraction or a multiple of π
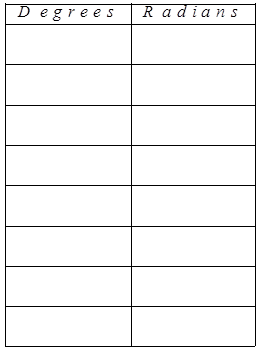
Since 180° is equal to πradians, angles in degrees thatcan be written as a fraction of180° can be converted inradians easily
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca
To convert from degrees to radians,multiply the value by:
To convert from radians to degrees,multiply the value by:
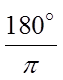
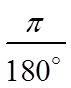

To convert degrees into radians, multiply the fractionby
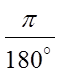
Ex: Convert the following to radian measure:
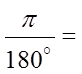
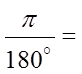
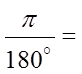
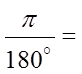
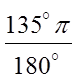
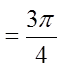
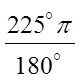
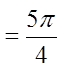
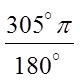
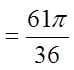
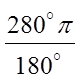
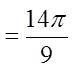
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca

In contrast, to convert from radians to degrees, multiplythe value by:
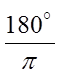
Ex: Convert the following to degrees:
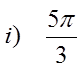
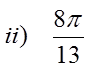
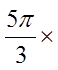
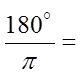
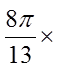
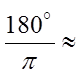
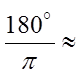
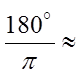
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca

IV) FINDING THE ARC LENGTH OF A CIRCLE
The arc length is a fraction of the circumference of the circle
The fraction is given by the central angle divided by the 2π
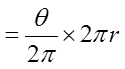
Central Angle
given in radians
If the central angle is given in degrees, you must convert itto radians!!
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca

Ex: An arc with a radius of 5m has a central angle of 2.5radians. Find the arc length.
Practice: An arc with a radius of 7m has a central angle of 177.4°. Find the arc length.
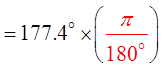
Convert the angle to radians!!
© Copyright All Rights Reserved. Homework Depot www.BCMath.ca
Practice: An arc with a radius of 2.4m has an arc length of5.3m. Find the central angle in radians and degrees.
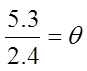
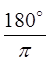
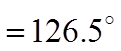

V) REVIEW: QUADRANTS & X /Y AXIS
Center: Origin (0,0)
On the X-axis:
Right – Positive
Left - Negative
On the Y-axis:
Up – Positive
Bottom - Negative
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) UNIT CIRCLES & ROTATIONS
A “unit circle” is a circle rotated around the origin with a radius of1 unit
The radius starts to rotate from the right side (Initial Arm)
The line rotating around the center is called a “Terminal Arm”
Rotated Counter clock-wise (positive angle)
Rotated Clock-wise (negative angle)
PositiveDirection
NegativeDirection
Initial Arm
Terminal Arm
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VII) ANGLES IN STANDARD POSITION:
All angles in “standard position” begin from the Initial arm(right)
The angle is created by rotating the Terminal arm aroundthe origin (counter-clockwise)
in standard position
Ex: Draw the following angles in standard position: a) 62° b) 152 °
in standard position
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Draw the following angles in standard position:
a) 312° b) -77°
in standard position
in standard position
© Copyright all rights reserved to Homework depot: www.BCMath.ca
c) 2.5π radiansd) 9.42 radians
in standard position
9.42 radians instandard position

VIII) CO-TERMINAL ANGLES
Angles that have their terminal arms at the same position
Co-terminal angles have a difference of 360° or multiples of360° (Full circles)
ie: 30°, 390°, 750°, -330°, -330°, -690°, ..etc
All these angles have the same
Position, “Co-terminal Angles”
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given the following angles, provide two co-terminalangles and a formula for all the co-terminal angles
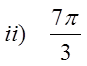
Add/subtract full circles
to get co-terminal angles
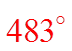
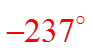
All co-terminal are sums/differences of 360°
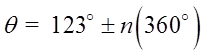
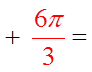
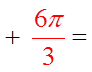
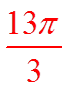
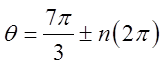
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IX) REFERENCE ANGLES
An angle created by the terminal arm and X-axis.
Reference angles must be in the same quadrant as theterminal arm
Ex: Given the following angles in standard position, find the
reference angle
in standard position
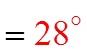
in standard position
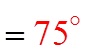
ReferenceAngle
ReferenceAngle
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Given each of the following terminal arms, indicatewhich is the reference angle:
NEITHER!!
NOTE: THE Reference angles must be formed with the X-axis and it must be in the same quadrant as the terminal arm
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Practice: Find the reference angle for each of the followingangles in standard position:
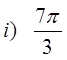
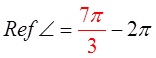
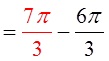
ReferenceAngle
Reference Angle
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: FIND THE REFERENCE ANGLE FOR EACH OFTHE FOLLOWING ANGLES IN STANDARD POSITION
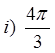
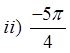
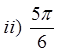
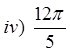
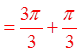
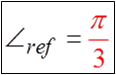
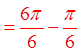
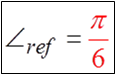
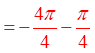
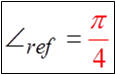
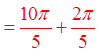
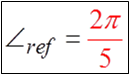
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IX) RECOGNIZING REFERENCE ANGLES
Angles with the same height will have the same reference angle
ie: 30°, 150°, 210°, and 330° all have the same reference angle at 30°
ie: 60°, 120°, 240°, and 300° all have the same reference angle at 60°
ie: 45°, 135°, 225°, and 315° all have the same reference angle at 45°
These angles all have thesame distance from theX-axis, so their Referenceangles are all equal
If we ever encounterthese angles, we can use Special triangles
© Copyright all rights reserved to Homework depot: www.BCMath.ca

RECOGNIZING SPECIAL ANGLES IN RADIAN FORM
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:
Assignment 3.1