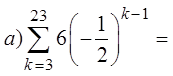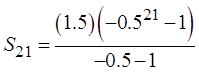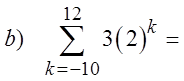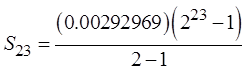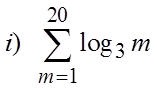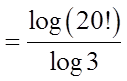SECTION 2.5 SIGMA NOTATIONSAND SUMMATION
i) Concept of Sigma Notation, number of terms
ii) Solving for Sums using Sigma Notations
iii) Problems involving Sigma Notations
iv) Sums of Sequences involving consecutivesquares, cubes, and powers
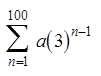
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) WHAT IS A SIGMA NOTATION:
A notation that represents a series (sum)
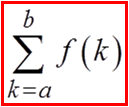
Function
Variable in thefunction
The value of “k”
in the last term
The value of “k”
in the first term
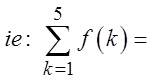
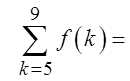
Note: The number of terms will be (b – a + 1)
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: EXPAND AND EVALUATE THE FOLLOWING SERIES:
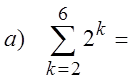
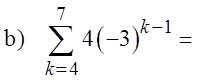
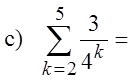
© Copyright all rights reserved to Homework depot: www.BCMath.ca

When a sigma notation contain too many terms, use theformulas from the Geometric series to find the sum
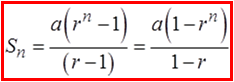
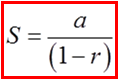
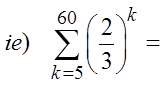
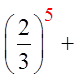
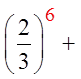
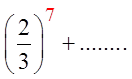
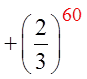
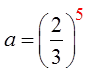
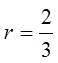
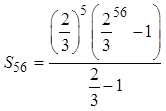
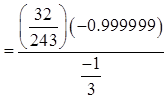
© Copyright all rights reserved to Homework depot: www.BCMath.ca


PRACTICE: EVALUATE EACH OF THE FOLLOWINGINFINITE GEOMETRIC SERIES:
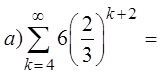
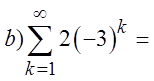
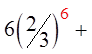
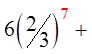
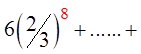
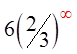
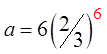
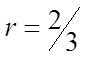
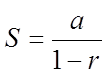
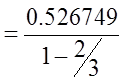
Since:
the infinite geometric series will
become infinity
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN THE FOLLOWING GEOMETRIC SERIES, REWRITEAS A SIGMA NOTATION:
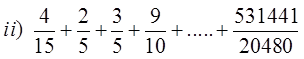


HOMEWORK:
Assignment 2.5