SECTION 2.4 RECURSIVESEQUENCES AND SERIES

i) Concept of Recursive Sequences

ii) Fibonacci Sequence

iii) Phone Tree

iv) Rabbit Population Question

© Copyright all rights reserved to Homework depot: www.BCMath.ca

WHAT ARE RECURSIVE SEQUENCES:

A recursive sequence is a sequence where each term (tn) isdefined from earlier terms (tn-1 or tn-2) in the sequence.

Examples:

2, 4, 6, 10, 16, 26, 42,….

2, 4, 7, 27, 188, …..

1, 2, -3, -5, -16, …..

 The Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ……

Ex: Given that t1 = 0, t2 = 3 and   tn= tn-1+2 (tn-2), find t7

Sum of the previous two terms

Product of the previous two terms minus one

tn = (tn-2)2 – (tn-1)2

Ex: Find the first 4 terms of the sequence

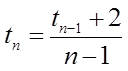
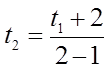
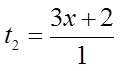
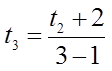
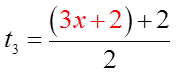
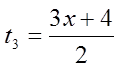
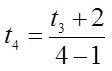
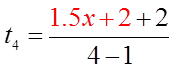
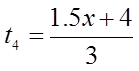
The first four terms will be:

APPLICATIONS OF RECURSIVE SEQUENCES:

Programming: C++, C

Using input from a previous code

Nature:

Plants, tree branches, flowers (# of leaves)

Golden Ratio/Fibonacci Numbers

Count the number ofbranches in each stage

The number of branchesin each stage is the sameas the Fibonacci sequence

Ex: A principle starts a phone tree by calling 2 teachers.Each teacher is to call two other teachers down the tree.  Ifthere are 500 teachers in the school and each call takes 2minutes, how long will it take to phone all the teachers ifthe first phone call started at 9:00pm?

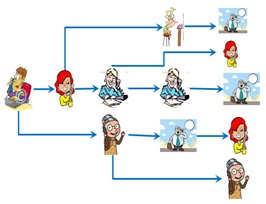
The number of teachers in each level is a recursive sequence:

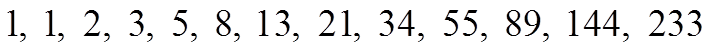
Each additional level will be an extra 2 minutes to contact everyone

Figure out at which level will a total of 500 people be contacted

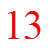
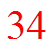
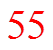
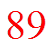
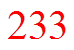
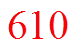
By the 13th level, all 500 teachers will be contacted

The amount of time to contact all teacher at the 13th level will be:

Therefore, all teachers will be contacted by 9:24pm.

Ex: What are the 4th, 5th and 6th terms of this sequence?