
SECTION 2.3GEOMETRIC SERIES
i) Sums of a geometric series and infinitegeometric series
ii) Deriving the formula for the sum of ageometric series and infinite geometric series
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) SUM OF GEOMETRIC SEQUENCE:
Sum of a geometric series up to the nth term
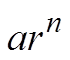
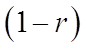
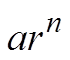
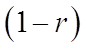
Multiply both sides by “r”
Subtract the equations!
Factor out “Sn”
Divide both sides by (1 - r)
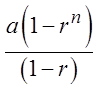
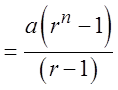
Factor out “a”
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE SUM OF THE FOLLOWING GEOMETRICSEQUENCE:


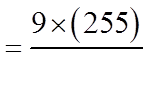
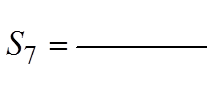

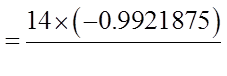
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE SUM:
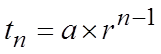
First find outhow many terms there are
Then find thesum up to the “14th”term
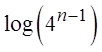
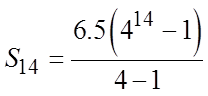
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: A RUBBER BALL IS DROPPED FROM A HEIGHT OF 10M. AFTEREACH BOUNCE, THE BALL RETURNS TO 65% OF ITS PREVIOUSHEIGHT. CALCULATE ALL THE VERTICAL DISPLACEMENT RIGHTBEFORE THE 8TH BOUNCE.
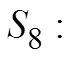
Note: There are two types ofdisplacement: Going up and down
Each displacement is doubled
except the first bounce
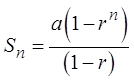
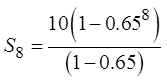
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Jason gave his son a penny on the first day of the monthand doubled the amount each day. How much moneywill he give his son altogether by the 30th day?
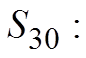

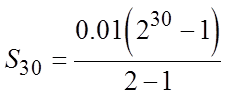
© Copyright all rights reserved to Homework depot: www.BCMath.ca

CHALLENGE: THE SUM OF THE SECOND & THIRD TERM IN AGEOMETRIC SERIES IS 45. THE SUM OF THE FOURTH & FIFTHTERM IS 20. FIND THE GEOMETRIC SEQUENCE:
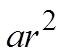
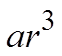
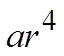
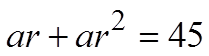
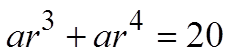
The 4th and 5th terms add to 20
The 2nd and 3rd terms add to 45
Factor out any common factors
In each equation
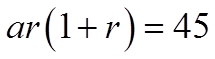
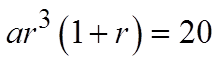
Divide the equations
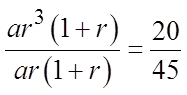
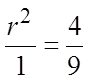
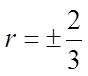
Use the common ratio to find the first term
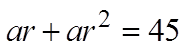
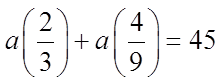
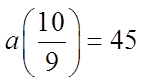
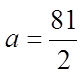
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Find the 2nd series when thecommon ratio is negative

I) WHAT IS AN INFINITE GEOMETRIC SERIES?
A Geometric series with an infinite number of terms
If the common ratio is greater than 1, each term will getbigger and the sum will soon add up to infinity
Note: Any infinite G.S. with a common ratio then the sum willadd up to infinity
Most infinite G.S. in sect. 2.9 will have a common ratiobetween -1 and 1
Each term in the series will get smaller
Eventually some terms will become so small such thatadding them will be insignificant, like adding zero
© Copyright all rights reserved to Homework depot: www.BCMath.ca

When the ratio is the infinite G.S. will converge to afixed value
These values are so small such that adding them will be insignificant!!
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) FORMULA FOR THE SUM OF AN INFINITE G.S.
If the Ratio is bigger than 1, the sum will be positive infinity
If the ratio is smaller than -1, the sum will be negativeinfinity
If the Ratio is between 1 and -1, the sum can be obtainedthrough a formula:
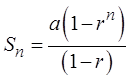
Formula for the sum of a G.S. with “n” terms
If there are infinite terms, then “n” will be infinity
Since
the value of
will be zero
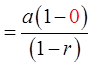
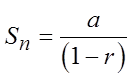
The equation will only apply if
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE SUM OF THE INFINITE G.S.
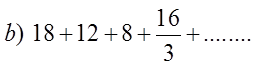
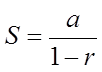
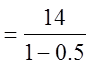
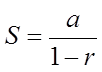
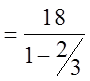
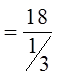
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: THE COMMON RATIO OF AN INFINITE GEOMETRICSERIES IS 0.75. IF THE SUM OF ALL THE TERMSCONVERGES TO 20, FIND THE FIRST TERM.
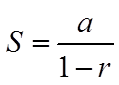
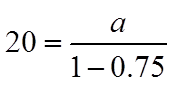
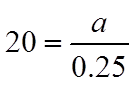
© Copyright all rights reserved to Homework depot: www.BCMath.ca

GIVEN THE FOLLOWING INFINITE GEOMETRICSEQUENCE, WHAT SHOULD THE VALUE OF “R”BE SO THAT THE SUM WILL BE 20?
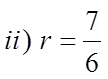
The series must be converging
So the value of “r” must be between -1 and 1
The answer must be r = 0.80
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: A MOVIE IN A THEATRE GENERATE $250,000 INREVENUE IN THE FIRST MONTH OF ITS SHOWING. EACHMONTH, SALES FROM THAT MOVIE DROP BY 15%. IF THEMOVIE IS SHOWN FOR A LONG TIME, WHAT IS THE TOTALREVENUE GENERATED?
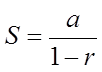
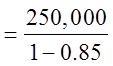
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:
Assignment 2.3