SECTION 2.2 GEOMETRICSEQUENCES

i) Terms, common ratio, number of terms in ageometric sequence

ii) Geometric means

iii) Solving Algebraic sequences

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) WHAT IS A GEOMETRIC SEQUENCE?

A sequence where each term after the first is multipliedby a common ratio “r”

Not the same as an arithmetic sequence (Add)

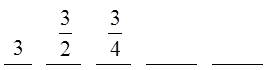
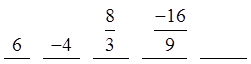
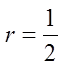
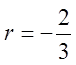
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) FORMULA FOR GEOMETRIC SEQUENCE:

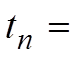
The value of the “nth” term

Value of the 1st  term

Common Ratio

The rank of the term

- Divide any term by its previous term

© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN THE FOLLOWING SEQUENCE, FIND THE 20TH TERM:

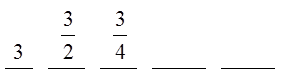
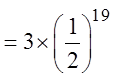
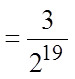
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN THE THREE TERMS IN A GEOMETRIC SEQUENCE,FIND THE COMMON RATIO:

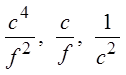
To find the common ratio, you can just takeany term and divide it by the previous term

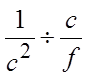
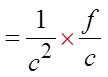
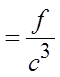
So, the common ratio will be:

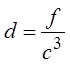
EX: THE THIRD TERM OF A GEOMETRIC SEQUENCE IS 27 AND THESIXTH TERM IS 64.  FIND THE COMMON RATIO:

Each term in the sequence is equal to theprevious term multiplied by the common ratio:

The sixth term is equal to both 64 and 27r3

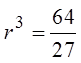
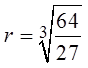
To find the terms in between, just multiply  27 by the common ratio.

© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN             AND              FIND THE COMMON RATIO AND THEFIRST  TERM:

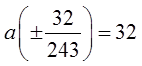
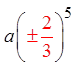
Now solve for

the first term

HOMEWORK:

Assignment 2.2