
SECTION 2.1 ARITHMETICSEQUENCES AND SERIES
i) Solving for Terms and Sums of an arithmeticsequences
ii) Problems involving A.S.
© Copyright all rights reserved to Homework depot: www.BCMath.ca

ARITHMETIC SEQUENCES:
A sequence with a pattern, where each term increases ordecreases by a common difference (d)
Ie: For each of the following sequences, find the commondifference if it is arithmetic:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOW DOES AN ARITHMETIC SEQUENCE WORK?
The first term of an A.S. is called “a” or “t1”
Each term after the first adds another common difference “d”
The value of each term is denoted “tn”, where “n” is the order ofthe term
The number of common differences “d” in each term is one lessthan it “n” value
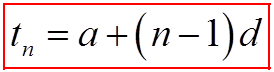
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX#: SOLVE EACH OF THE PROBLEMS BELOW
Find the 30th term in the sequence:
Find the 200th term in the sequence:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX#: SOLVE EACH OF THE PROBLEMS BELOW
What term is -523 in the arithmetic sequence?
Find the 3 missing terms in the arithmetic sequence:
–523 is the65th term!
Therefore, the numbers will be:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

FORMULA FOR THE SUM OF AN ARITHMETIC SEQUENCE:
The sum of an arithmetic series up to the “nth” term isdenoted “Sn”
If we group the first with the last term and also every termin between, we will have n/2 number of equal pairs
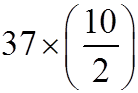
If we group the first and last term, the value will be equal to 2a+(n–1)d
The sum will then be the value of each pair times the number of pairs
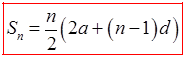
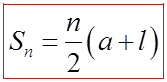
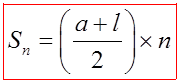
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE SUM UP TO THE 10TH TERM:
Use the General Term Formula to find the last term
EX: FIND THE SUM UP TO THE 100TH TERM:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE SUM OF THE ARITHMETIC SERIES:
Find out how many terms there are byusing the General Term formula:
Find the Sum with theFormula:
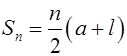
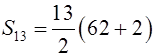
Since it’s an arithmetic series, then (t3 – t2 )= (t4 – t3 ) = d
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex#) If the sum of the first 50 odd numbers is equal to “S”and the sum of the first 100 even numbers is equal to T,then what is the value of “T – S”?
© Copyright all rights reserved to Homework depot: www.BCMath.ca
