SECTION 1.4DERIVING QUADRATIC EQUATIONS

i) Find the Q. E. when given two points or roots,one root is double/triple 2nd root

ii) Intersection b/n two parabolas

iii) Perfect Trinomialsiv) For what values of “k” will there be 2roots,1 root, or no roots

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) DERIVING A QUADRATIC FUNCTION

When given the roots we can find the equation of thequadratic function by substituting them in factoredform

Ie: If the roots of a quadratic function are –3 and –2/3,the equation in factored form will be:

To find the constant “a” plug in the coordinates ofanother and solve for “a”

Ex: Find the equation of a parabola with a vertex at (-2,3)and y-intercept at 6.

1st: When the vertex is given,constants “p” and “q” are also given

2nd: We need an additional point to find the missing constant“a”.  Plug the coordinates and solve for “a”

Coordinates of y intercept is (0,6)

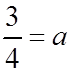
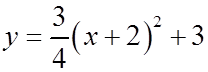
The equation is ofthe parabola is:

Practice: Find the equation of a parabola with a vertexat (5,2) and passing point (3,4).

Coordinates of point is (3,4)

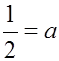
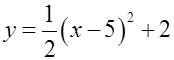
Ex: Write the equation of a parabola with a maximumvalue of 5 at x= –4 and is congruent to

The equation is of the parabola is:

Has a Maximum Value, so it opens down

Maximum value of 5 at x = –4

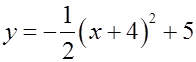
The equation is of the parabola is:

III) FINDING MISSING CONSTANTS WHEN ONE ROOT ISDOUBLE/TRIPLE THE OTHER

Preview: Find the value of  “k”

Solve the equation with one missingvariable first.  You can’t solve anequation with two unknowns!!!

The coefficients of x2, x, and constantterm must be equal

Given a formula with a missing constant “K” and told thatone root is either “Double” or “Tripled” the other

Let the first root be “r” and the second root be “2r” or “3r”

Rewrite the equation in factored form

FOIL (Expand)

Compare the coefficients x2, x, and constant to solve for “K”

EX: GIVEN THE EQUATION:WHERE ONE ROOTS IS DOUBLE THE OTHER, FIND “K”

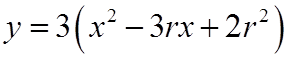
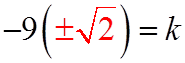
EX: GIVEN THE EQUATION:WHERE ONE ROOTS IS TRIPLE THE OTHER, FIND “K”

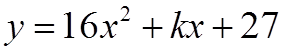
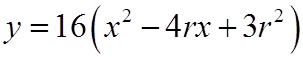
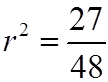
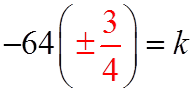
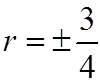
II) REVIEW INEQUALITIES:

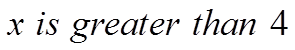
Whenever you divide or multiply by a negative number,the inequality sign will switch sides

SOLVING INEQUALITIES WITH SQUARES:

When you have inequalities with squares,isolate the square and then square root both sides

Draw a number line, draw the roots on the numberline

You will get three different domains on the numberline

Pick a value from each domain and check if itsatisfies the inequality

Domains that satisfy the equality will be yoursolution

EXAMPLE: SOLVE THE FOLLOWING INEQUALITIES:

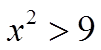
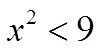
PRACTICE: SOLVE THE FOLLOWING INEQUALITIES:

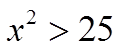
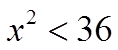
III) NATURE OF ROOTS (SOLVING FOR “K”)

Ex: For what values of “k” does the equation havetwo different real roots?

Since the equation has 2 differentreal roots, The discriminant must begreater than zero

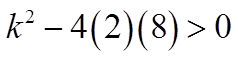
IF “K” is less than -8 or greater than 8, the quadraticequation will have two X-intercepts

Practice: For what values of “k” does the equationhave          a) Two equal roots     b)No real roots

a) Since the equation has 2equal roots, The discriminantmust be equal to zero

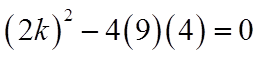
b) No real roots discriminantmust be less than zero

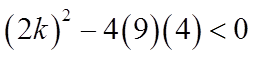
IF K equals 6 or -6, theequation will have adouble root!

IF K is between 6 or -6,the equation will nothave any roots

HOMEWORK:

Assignment 1.4