
SECTION 1.3PROBLEM SOLVING INVOLVINGMAX AND MIN
i) Revenue problems
ii) Maximum area
iii) Minimum for sums of two squares
© Copyright all rights reserved to Homework depot: www.BCMath.ca


I) BASICS IN OPERATING A BUSINESS!
When we increase the price of an merchandise, Sales willdecrease
In contrast, when we decrease the price sales will increase
Revenue is the income generated from sales
In this lesson, we will learn to Maximize Revenue and Profit

© Copyright all rights reserved to Homework depot: www.BCMath.ca
Ex#1) An ice-cream shop sells 300 cones a day at $3.50 each.For every $0.50 increase, he loses 20 sales.
Q:How does the price affect quantity?
Q:How can the price be changed to generate the maximumrevenue?


ANALYZE THE QUESTION: PRICE VS QUANTITY
Initial Quantity:
Initial Price:
Change in Quantity:
Change in Price:
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Sales begin at 300 cones per day
The initial price is at 3.50 per cone
Decrease of 20 cones in sales
Price is increased by $0.50/cone












































3.5
4
4.5
5
5.5
200
300

Initial value
For every increase in 50 cents:
Sales will decrease by 20 units
For every change, a new set ofcoordinates will be created
The points can be used tomake a straight line
Use the slope equationto find how the priceaffects quantity
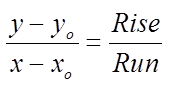

A) HOW DOES THE PRICE AFFECT QUANTITY?
If we plug in the values and Isolate “Q”, we obtain an equation thatshows how the price affects quantity
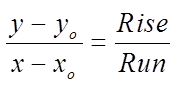
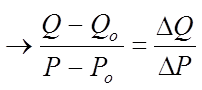
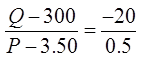
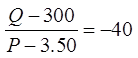
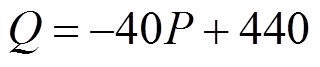
© Copyright all rights reserved to Homework depot: www.BCMath.ca
The x-axis corresponds with the price
The y-axis corresponds with the quantity
This equation shows how theprice affects the quantity

B) WHAT PRICE WILL GENERATE MAXIMUM REVENUE?
Revenue = Quantity x Price
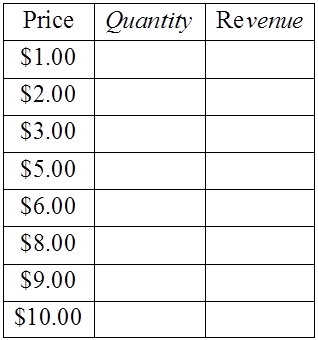
© Copyright all rights reserved to Homework depot: www.BCMath.ca














































1
2
3
4
5
6
7
8
9
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
The points come togetherand generate a parabola
The maximumrevenue will be at thevertex (highest pointon the graph)
Maximum revenue occurs whenthe price is at $5.50

FINDING THE MAXIMUM REVENUE
We can find the maximum revenue by CTS or XAV
The vertex of the revenue equation indicates themaximum revenue: x-coord: Price , y-coord: Revenue
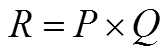
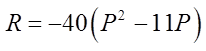
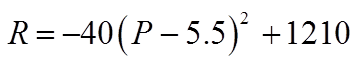
The Max revenue is $1210
The Maximum revenue occurswhen the price is at $5.50
CTS with the revenue equation
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX#2) A BROADWAY MUSICAL SELLS 3500 TICKETS A WEEK AT$25 PER TICKET. FOR EVERY $1.25 DECREASE, 400 EXTRATICKETS WILL BE SOLD.
Write “Q” as a function of “p”
Write “P” as a function of “Q”
Write “R” as a function of “p”
What price will generate the maximum revenue?
What Price will generate a Revenue greater than $80,000
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Use this chart to generate the equation:

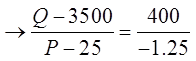
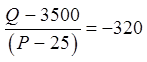
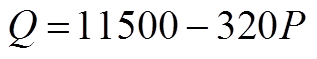

Write “P” as a function of “Q” (Isolate “P”)

© Copyright all rights reserved to Homework depot: www.BCMath.ca
Write “P” as a function of “R” and find the maximum revenue
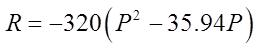
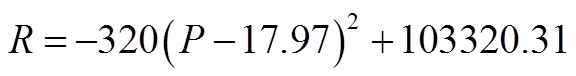
The Maximum Revenue is$103320.31 and when theunit price is $17.97

WHAT PRICE WILL YIELD A REVENUE GREATER THAN $80,000?
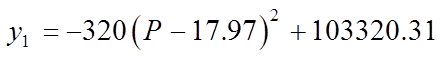
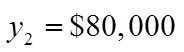
Find the Intersection Point
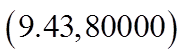
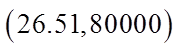
For any price between$9.43 to $26.51, therevenue will be greaterthan $80,000!!
© Copyright all rights reserved to Homework depot: www.BCMath.ca
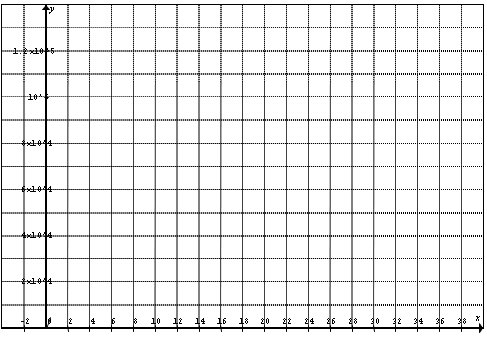

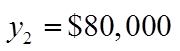
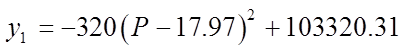
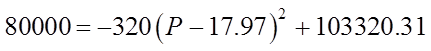
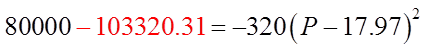
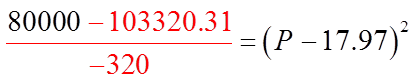
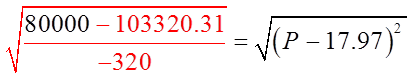
To solve for theintersection points,make the Revenueequal to $80,000 andsolve for the price
Isolate “P”
The Revenue will begreater than $80,000 ifthe price is between$9.43 to $26.51
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) MAX/MIN FOR NUMBER PROBLEMS
Use the information given to create a quadraticequation
Use CTS or XAV to find the vertex
Sum Add Difference Subtract
Product Multiplication
Squares Square the number
Ex: The sum of two numbers is 80. Their product is amaximum. Find the numbers
The sum is 80
They have a “product”that is a maximum
Substitute the firstequation into the secondone.
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Find the vertex because
the vertex is the maximum
1. Complete the square
2. Xavier
The maximum is 1600,when x = 40 and y = 40
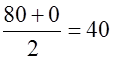
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: The difference of two numbers is 10. The sum oftheir squares is a minimum. Find the numbers
The difference is 10
The sum of their squares isa minimum
Substitute the first equationinto the second one.
Complete the square
The minimum occurswhen x = –5
The other number is:
Sum of the squares is:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX#3) A FARMER WANTS TO BUILD A RECTANGULAR BARN USING 100METERS OF FENCING FOR HIS COWS AND CHICKENS. HOWEVER, HENEEDS TO SEPARATE THE TWO GROUPS OF ANIMALS AND NEEDS TOMAKE THE LARGEST POSSIBLE AREA. DETERMINE THE DIMENSIONSFOR THE BARN.
ISOLATE ONE VARIABLE
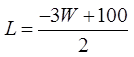
Complete the square
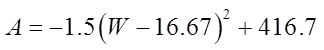
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK: ASSIGNMENT 1.3
© Copyright all rights reserved to Homework depot: www.BCMath.ca