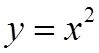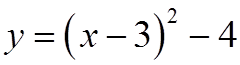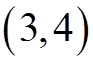SECTION 1.2QUADRATIC FUNCTIONS
i) Completing the square
ii) Graphing y=a(x-p)2+q
iii) Using a,p,q to find vertex, opens up, down,congruency factor,
iv) Deriving and using the quadratic function
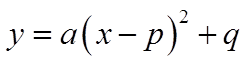
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) GRAPHING QF:
A Quadratic function in standard form is much easierto graph
Using constants “a”,”p”, & “q”, we can find the vertex,which way it opens and the congruency value
Vertex: Axis of Symmetry:
Domain:Range:
Y intercept: make x=0, solve for y
X-intercept: make y=0, solve for x
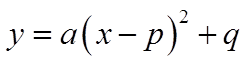
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FOR EACH OF FOLLOWING EQUATIONS, FIND THECONSTANTS “A”, “P”, “Q”, VERTEX, AND A.O.S.
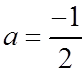
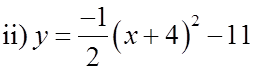
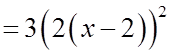
© Copyright all rights reserved to Homework depot: www.BCMath.ca

II) CONSTANTS “P” AND “Q”
The constant “p” affects the graph horizontally
When p=0, the graph is centered on the Y-axis
























x
y
0
























x
y
0
























x
y
0
2 unitsRight
2 unitsLeft























x
y
0























x
y
0
2 unitsup
2 unitsDown
InteractiveApplet
The constant “q” affects the graph vertically
© Copyright all rights reserved to Homework depot: www.BCMath.ca




III) HOW DOES THE CONSTANT “A” WORK?
5
5
3
3
1
1
Beginning at the vertexwe can graph all theother points withoutmaking a TOV
Each point increaseshorizontally by 1but increases verticallyby 1 , 3 , 5 , 7 , 9, …
7
7
© Copyright all rights reserved to Homework depot: www.BCMath.ca


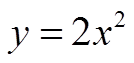
6
10
10
6
2
2
If “a = 2”, the pointsgo up faster.
Each point increaseshorizontally by 1but increases verticallyby 2 , 6 , 10 , 14 , 18, …

Simply multiply thevalues by “2”
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) CONSTANT “A” (CONGRUENCY FACTOR)
The constant “a” determines the (congruency) width ofthe parabola and which way it opens
If “a” is positive (Opens up)
If ‘a” is negative (Opens down)
If “a” is big (Skinny)
If “a” is small (Wide)
Congruency Factor:
The constant “a” can be used to determine how fastthe points on the parabola go up by
© Copyright all rights reserved to Homework depot: www.BCMath.ca


PRACTICE: GRAPH THE FOLLOWING PARABOLAS ANDINDICATE THE VERTEX, AOS, DOMAIN & RANGE
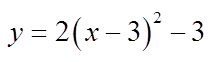
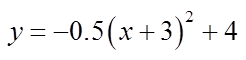

2
6
10

3.5
2.5
1.5
0.5
© Copyright all rights reserved to Homework depot: www.BCMath.ca

VI) CTS: COMPLETE THE SQUARE!
Completing the Square is a process that changes aquadratic functions from
General form: Standard Form:
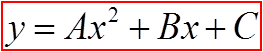
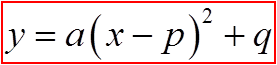
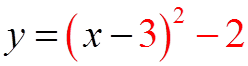
Bracket the first two terms!
Divide the second term by 2 andsquare it! The purpose is to make theexpression in the bracket into aperfect square!
Take the negative square outside ofthe brackets!
The trinomial becomes two equalbinomials
Standard Form!
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: CONVERT THE FOLLOWING TO STANDARD FORM
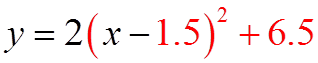
Bracket the first two terms!
Divide the second term by 2 andsquare it!
Take the negative square outside ofthe brackets and multiply withcoefficient in front!
The trinomial becomes two equalbinomials
Standard Form!
Factor out any coefficient for x2
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK: ASSIGNMENT 1.2
© Copyright all rights reserved to Homework depot: www.BCMath.ca