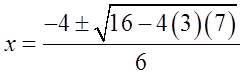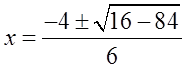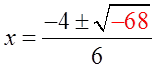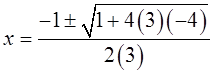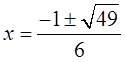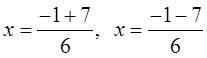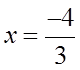SECTION 1.1QUADRATIC FUNCTIONS
i) Xavier Method – Finding roots by factoring, vertexand axis of symmetry by average of roots
ii) Domain and Range of QF
iii) Quadratic Formula
iv) Discriminant and the number of roots
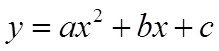
© Copyright all rights reserved to Homework depot: www.BCMath.ca

REVIEW: LINEAR AND QUADRATIC FUNCTIONS
Linear Functions
Straight Lines
General Form:
Highest degree for “x” is one
Quadratic Functions
Curved
Shape of a “Parabola”
Highest Degree for “x” is two
General Form:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) WHY IS A QUADRATIC FUNCTION U-SHAPED?
If we make a TOV, plot the coordinates, and connectthe dots, the resulting shape is a Parabola
© Copyright all rights reserved to Homework depot: www.BCMath.ca

x
y
0
II) COMPONENTS OF A PARABOLA
Vertex: The tip of theparabola
Axis of Symmetry: A linethat cuts the graph inhalf (middle)
X intercepts: intersectionpoint between graph andthe x axis
Y intercept: intersectionpoint between graph andthe y axis
© Copyright all rights reserved to Homework depot: www.BCMath.ca

x
y
-1
0
1
2
3
4
5
6
7
1
2
3
4
x
y
-1
0
1
2
3
4
5
6
7
-4
-3
-2
-1
GRAPHING PARABOLAS WITH XAVIER’S METHOD
First find the vertex using X.A.V.
X: x-intercepts by factoring
A: Axis of Symmetry (average of x intercepts)
V: Vertex by substituting AOS into formula
Use the constant “a” to determine which way the graphopens
Plot a couple of extra points for a better graph
For Quadratic Functions that do not have x-intercepts, wewill learn to graph them in the next section


© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE X INTERCEPTS, AXIS OF SYMMETRY,VERTEX AND GRAPH
1st Factor: X intercepts
2nd Axis of Symmetry (Equation)
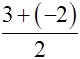
3rd Vertex: (Coordinates)
At the x-intercept, they-coordinate is zero
The A.O.S. is in the middlebetween the two x-intercepts!!(AVERAGE)
The A.O.S. and vertex hasthe same x-coordinate.
© Copyright all rights reserved to Homework depot: www.BCMath.ca

GRAPH:

2. Vertex
3. Plot several morepoints to get an accurategraph
1. X Intercepts: (-2,0) & (3,0)
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: FIND THE X INTERCEPTS, AXIS OFSYMMETRY, VERTEX AND GRAPH
1st Factor: X intercepts
2nd A.O.S.
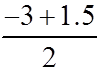
3rd Vertex
© Copyright all rights reserved to Homework depot: www.BCMath.ca

GRAPH:

2. Vertex
1. X Intercepts: (-3,0) & (1.5,0)
© Copyright all rights reserved to Homework depot: www.BCMath.ca

III)THE QUADRATIC FORMULA:
We need to factor a quadratic equation in order tofind the x-intercepts
To do this, use either the BUM Method, Criss-CrossMethod, or Grouping Method
However, if a quadratic equation can not be factored,use the “Quadratic Formula”
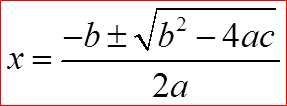
Can’t Divide by zero!
Can’t square root anegative number
If the value is negative, thenthere are no “x” intercepts
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Ex: Use the Quadratic Formula to find the exact valuesof “x”
First: Find coefficients
Plug coefficients into formula:
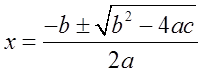
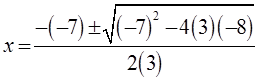
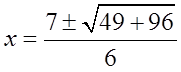
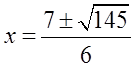
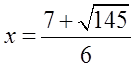
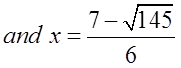
You get two answersbecause of +


IV) DISCRIMINANT AND NATURE OF THE ROOTS
To determine the “Nature of the Roots” of a QF(aka: the Number of X-intercepts), find the value of thediscriminant
A Quadratic function can have either
2 distinct roots(2 different x intercepts)
2 equal roots(1 distinct root OR double roots)
No real roots(no x intercepts)
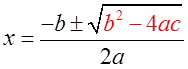
x
y
-2
-1
0
1
2
x
-
-
0
x
y
-2
-1
0
1
2
4
x
y
-1
0
1
2
3
4
x
0
4
x
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: DETERMINE THE NATURE OF THE ROOTSFOR EACH EQUATION: (DO NOT SOLVE)
Discriminant isnegative There areno real roots
Discriminant ispositive There are 2real roots
© Copyright all rights reserved to Homework depot: www.BCMath.ca

III) WHERE DOES THE QF COME FROM?
Take the equation: andComplete the Square. Then Isolate “x”
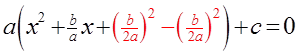
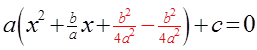
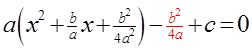
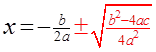
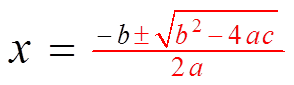
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK: ASSIGNMENT 1.1
© Copyright all rights reserved to Homework depot: www.BCMath.ca