SECTION 4.5ABSOLUTE VALUE ANDRECIPROCALS OF POLYNOMIALFUNCTIONS

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) REVIEW

Line Equation:

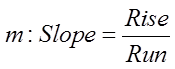
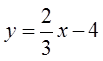
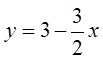
II) ABSOLUTE VALUE FUNCTION

The absolute value of any real number willbecome positive

Negative  Positive

Positive  Positive

Note:  An absolute value function will take anypoint with a negative y-coordinate and change itto a positive y-coordinate

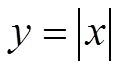
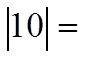
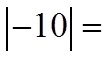
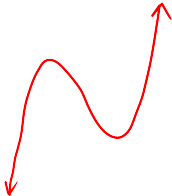
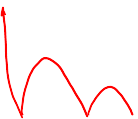
III) GRAPHS OF ABSOLUTE VALUE FUNCTIONS

The ABS function will reflect any part of the functionunder the x-axis to above the x-axis

The ABS of a straight line is a V-shape

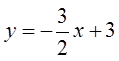
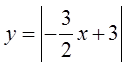
The center of the graph is atthe x-intercept

There are two sides: Left & Right

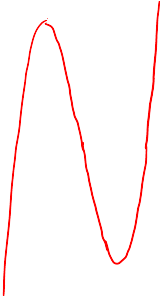
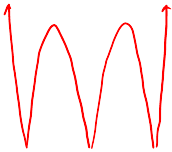
ABSOLUTE VALUE OF CUBIC FUNCTIONS

Suppose you’re given the graph of the polynomial

Parts of the graph under the x-axis will be reflected up

x

y

-3

-2

-1

0

1

2

-4

-2

2

4

6

x

y

-5

-4

-3

-2

-1

0

1

2

3

4

5

-10

-8

-6

-4

-2

2

4

6

8

10

IV) SOLVING ABSOLUTE VALUE EQUATIONS

When solving abs equations, the value inside the abssign can be both positive or negative

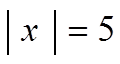
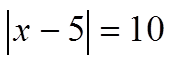
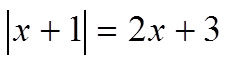
So when we are solving abs functions, we need toconsider both cases

After we solve for “x” in both cases, plug it back into theequation to check for extraneous roots

Extraneous roots will occur when the y-value isnegative

x

y

-10

-8

-6

-4

-2

0

2

4

6

-2

2

4

6

The solutions are: x= -8 & x= 2

Now check for extraneous roots byplugging “x” back into the originalequation

If we are to solve this equationgraphically:

PRACTICE: SOLVE

No Solutions

There is only onesolution  at x = 0

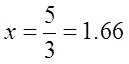
There is only onesolution at x = 1.666…

Extraneous Root

PRACTICE: SOLVE

x

y

-3

-2

-1

0

1

2

3

4

5

6

-2

2

4

6

x

y

-3

-2

-1

0

1

2

3

4

5

6

-2

2

4

6

Only one intersection at x=0

Only one intersection at x=1.66

Extraneous

Root

V) SOLVING ABSOLUTE VALUE INEQUALITIES

Solve for all intersections points

Number Line  Test Points

Check which Domain satisfies the inequality

Solve for Intersections points

Make a number Line

Create Test Points

Only one region satisfythe inequality

PRACTICE: SOLVE THE INEQUALITIES

Extraneous Root

b/c right side willbe negative

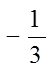
Soln.

Soln.

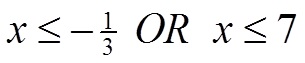
CHALLENGE:

Both sides of the numberline yield no solutions.  Sothe only point that satisfies theinequality is at x = –2

No Solution!

There are no intersection pointsSo we only need one test point

Extraneous

Solution: X can be all real numbers