SECTION 8.3  (PART 1)ANGLE PROPERTIES IN A CIRCLE

© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) TERMS

Central Angle: (aka Sector Angle) An angle created by two radii’s.

A central angle must be at thecenter of the circle

Inscribed Angle

An angle created by two chords

Inscribed angles must be on thecircumference of the circle

              “contains” / “subtends” chord AB

              “contains” / “subtends” chord CD

© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: GIVEN THE FOLLOWING DIAGRAM, FIND THEALL THE CENTRAL AND INSCRIBED ANGLES

Central Angles

Inscribed Angles

II) PROPERTY #1) DIAMETER INSCRIBES  90° ANGLE

1. The inscribed angle of a semi-circle (diameter) is equalto 90°

Link to Semi-Circle Applet

In contrast, if the inscribedangle  is 90°, the chordcontained must be a diameter

© Copyright all rights reserved to Homework depot: www.BCMath.ca

Here’s a proof why this angle is 90°if it is contained by the diameter

II) PROOF FOR PROPERTY #1)

Draw a radius to the corner

Now we have 2 isosceles triangles

All 3 angles in a triangle add to 180°

This angle is “a” + “b”

Ex: Find the value of “x” in each diagram:

“x” is the length of the radius

Since the angleis 90°  it  must be

a right triangle

Use the Pythago-rean  thm. to findthe diameter

“x’ is half the diameter

The triangle on the left is anisosceles triangle b/c two sidesare made with the radius

The angle at the top is 90°because it is inscribed by thediameter

2. Central Angles containing equal chords/arcs are equal

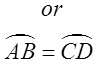
In contrast, if the central angles were equal, then the arcs andchords must also be equal

© Copyright all rights reserved to Homework depot: www.BCMath.ca

Suppose the two chords were equalin length: AB and CD

OR even the chords that they subtend

Then the central angles contained by thechords/arcs will be equal in value

Reason: when you rotate the chord or arc, the central angledoesn’t get any bigger or smaller.  It stays the same

FIND THE VALUE OF THE “X”:

Since the chord are equal inlength the central angles thatcontain are also equal

Therefore, angle “x” is equal to 65°

The sum of all the angles in astraight line add to 180°

So the angle at the top is equalto 64°

If the central angles are equalthen the chords they containare also equal

HOMEWORK:

Assignment 8.3A