
SECTION 8.2CHORD PROPERTIES
© Copyright all rights reserved to Homework depot: www.BCMath.ca

I) PROPERTIES OF A CIRCLE
Chord: A line with two endpoints on the circle
Chord
Secant: A line that intersects a circle at two different points
Secant
Diameter: A chord with the midpoint on the center of the circle
Radius: A line that runs from the center to the edge of the circle
Segment: Area in a circle separated by the chord (Watermelon)
Segment
Sector: Area in a circle separated by two radii’s (Pizza)
Sector
Arc A fraction of the circumference
Major Arc: Arc over 50% of the circumference
Minor Arc Arc less than 50% of the circumference
Minor Arc
Major Arc
Click Here for Circle Applet
© Copyright all rights reserved to Homework depot: www.BCMath.ca

NAMING CHORDS AND ANGLES:
When naming chords, use the endpoints of chord
When naming angles, the letter where the angle is willbe in the middle. The other two letters will be the otherendpoints of the lines

There are 3 main chord properties: If any two is true, thethird one must also be true
#1) If a Line through the centerof the circle is perpendicularto the chord, then it must bisectsthe chord (cut it in half)
The two sides of the chord have equal length
II) CHORD PROPERTIES:
Ex: If AB is 10cm long, how long is AC?
Chord Property #1


#2) If a Line through the center
of the circle bisects the chord ,
then it must be perpendicular
to the chord
The chord (black) cross the red line at 90°
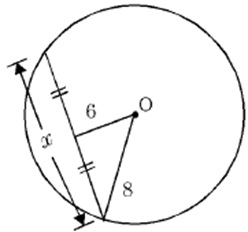
Ex: Find the value of “x” in the diagram:
The angle is 90° because of the2nd chord property
Use the Pythagorean Thm to find the base
y


If a Line bisects and isperpendicular to a chord, then itmust cross the center of the circle
Somewhere along the red line, thecenter of the circle will be on it
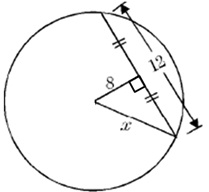
Ex: Given the following circle, what is the length of thediameter?
We know that this point is the centre of thecircle because of the 3rd Chord Property
The base of the triangle is 6 units long
6
Pythagorean Triple 6, 8, 10, so “x” is equal to 10
If the radius is 10, then the diameter is 20


II) CARPENTERS METHOD
How to Find the center of a Circle
Draw two chords
Draw the Perpendicular bisector of each chord
The Perpendicular bisectors will cross at the center ofthe circle
The perpendicular bisectorsof any two chords in a circle
will always intersect at the
center of the circle
© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: FIND THE MISSING SIDE “X”
All radii’s in a circle are equal
The chord is bisected, so both sidesmust be equal
Since the line through the center isbisecting the chord, it must cross at90°
Right Triangle Pythagorus
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: FIND THE MISSING SIDE “X”
All radii’s in a circle are equal
Since the line through the center isperpendicular to the chord,it must bisect it.
Add another radii to create a rightTriangle
© Copyright all rights reserved to Homework depot: www.BCMath.ca
