
SECTION 1.4SURFACE AREAS OF OTHERCOMPOSITE SOLIDS
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

REVIEW: AREAS OF TRIANGLES AND CIRCLES
Area of a Triangle – Base times Height divided by 2
The base and height must be perpendicular
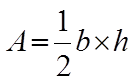
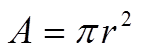
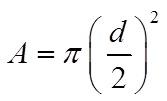
Area of a Circle = x r x r
= 3.14159162
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

SURFACE AREA OF CYLINDERS & TRIANGULAR PRISMS

The base of a cylinder is a circle
The surface area of a cylinder is the areaof all the sides
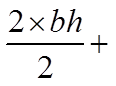
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

PRACTICE FIND THE SURFACE OF THE FOLLOWING SOLIDS:

Copyright All Rights Reserved Homework Depot at www.BCMath.ca


SURFACE AREAS OF COMPOSITE SOLIDS
A composite solid is a shape with two or solids combined
Two methods for finding the surface area of a compositesolid
1st Method:
Draw the faces of all six sides
Find the area of each side, then find the sum
2nd Method:
Find the surface area of each solid
Subtract the areas that are covered
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

EX: FIND THE SURFACE AREA OF THE GIVEN SOLID
Cut the solid into two piecesand draw the sides
Copyright All Rights Reserved Homework Depot at www.BCMath.ca


Place the circle on top of the
rectangle to get a complete side
shaded
Add all the sides up to find thesurface area of the solid

PRACTICE: FIND THE SURFACE AREA OF THE SOLID
Copyright All Rights Reserved Homework Depot at www.BCMath.ca
Find the area of eachrectangular prism
Then subtract all the sidesthat are covered!

HOMEWORK:
P40, 41 #3, 4, 5, 8, 9
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

AREA OF A CIRCLE:



To find the area of a circle, cut it into 8 equal pieces
Put the pieces together to create a parallelogram
The length of the top is equal to half the perimeter
The height is equal to the radius of the circle
