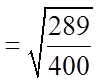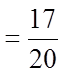SECTION 1.1SQUARE ROOTS OF PERFECTSQUARES
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

Perfect Squares: A number that is equal to the ‘square’of another number
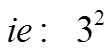
Therefore, “9” isa perfect square
Ex: Find the perfect squares for each of the following
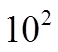
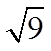
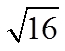
The square root of a
Perfect square will be an integer!
These are all Perfect Squares!!
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

EX: GIVEN THE FOLLOWING INTEGERS, INDICATEWHICH OF THE FOLLOWING IS A PERFECT SQUARE:
You can’t Square Root
a negative value!
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

FRACTIONS AS PERFECT SQUARES:
A fraction can also be a perfect square if both thenumerator and denominator are perfect squares
Remember to simplify and cancel out any commonfactors
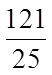
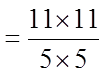
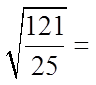
Divide them both by theGreatest Common factor “2”
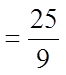
After the fraction is simplified,
we can see that both the top andbottom are perfect squares
Note: As long as both the numerator and denominator areboth perfect squares, then the fraction is also a perfect square
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

EX #2) WHICH OF THE FRACTIONS ARE PERFECT SQUARES
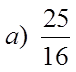
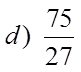
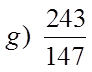
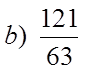
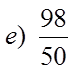
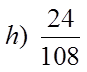
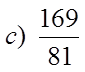
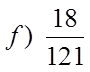
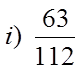
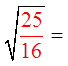
Top is aPS but thebottom isnot!
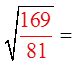
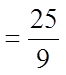

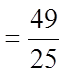
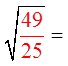
Bottom isa PS butthe top
is not!
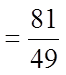
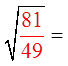
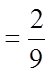
Bottom is aPS but thetop is not!
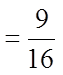
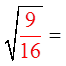
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

III) WRITING PERFECT SQUARES AS FRACTIONS
Note: When a fraction is written over 10, 100, 1000, …it can be easily converted to decimals
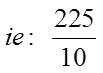
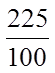
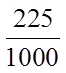
A fraction is a perfect square when both the numeratorand denominator are both perfect squares
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

EX#4) WHEN GIVEN THE AREA OF THESQUARE, FIND THE SIDE LENGTH
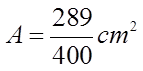
Copyright All Rights Reserved Homework Depot at www.BCMath.ca
The side length is equal to thesquare root of the area