
SECTION 7.1SQUARE AND SQUARE ROOTS
© Copyright all rights reserved to Homework depot: www.BCMath.ca

Perfect Squares: A number that is equal to the ‘square’of another number
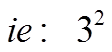
Therefore, “9” isa perfect square
Ex: Find the perfect squares for each of the following
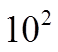
These are all Perfect Squares!!
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

EX: GIVEN THE FOLLOWING INTEGERS, INDICATEWHICH OF THE FOLLOWING IS A PERFECT SQUARE:
Perfect Squares can
not be negative!
Copyright All Rights Reserved Homework Depot at www.BCMath.ca

II) SQUARE ROOTS
The “Square Root” of a number is the opposite of“squaring” it
When finding the “square root” of a number, look for avalue that multiplies itself to equal it
For instance:
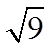
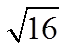
Because 3 time 3 equals 9
Because 4 time 4 equals 16
Ex: Find the square root of the following:
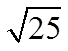
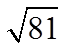
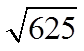
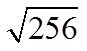
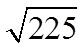
© Copyright all rights reserved to Homework depot: www.BCMath.ca

III) WHAT ARE FACTORS?
An integer which evenly divides a number withoutleaving a remainder
ie: What are all the factors of 24?
{1 , 2, 3, 4, 6, 8, 12, 24}
A number with only two factors are called:“Prime Numbers”
Ie: List the first 10 prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
© Copyright all rights reserved to Homework depot: www.BCMath.ca

IV) PRIME FACTORIZATION
A “decomposition” [break down] of a number where all itsfactors are prime numbers
Divide a number by all of its factors until all the factorsare prime numbers
Ex:: Find the Prime Factorization of the following numbers
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: FIND THE PRIME FACTORIZATION OF EACHNUMBER:
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRIME FACTORIZATION OF PERFECT SQUARES:
Find the prime factorization of each of the followingperfect squares:
What do you notice about the prime factorization ofperfect squares?
All perfect squares have an even number of primefactors
This is because there needs to be two of every factor tobe a perfect square
© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:
P 85 #7 to 13, 16, 18 to 21, and 25
© Copyright all rights reserved to Homework depot: www.BCMath.ca