6.4 Simulation and Expected Value

6.4 SIMULATION ANDEXPECTED VALUE

I) SIMULATIONS

A simulation is a way to replicate an experiment using adice/spinner/cards where each outcome corresponds with anevent with the exact same probability

Ex: Larry drives to work everyday using one of three differentroutes, taking either “Hastings Street”, “Kingsway ave”, or“1st Avenue”. If each route is chosen at random and equallylikely, which road will he take most often?

In this scenario, we can use a dice to simulate this experiment

For instance, if we roll a “1 or 2”, Larry takes Hastings

If we roll a “3 or 4”, Larry takes Kingsway.

If we roll a “5 or 6”, Larry takes 1st Avenue.

There are many other ways to simulate this experiment.

Given each scenario, create a simulation:

1: There are 3 black chairs, 6 red chairs, and 9 blue chairsin a circle. One person walks and randomly picks a chairto sit on. Create a simulation for which chair color thatperson will sit?

2: Jason have 2 pairs of shoes, 6 pairs of pants, and 8 shirts.Create a simulation for what outfit he should wear?

You can roll a die: If you roll a 1  pick the black chairs

If you roll a 2 or 3  pick the red chairs

If you roll a 4, 5, or 6  pick the blue chairs

Flip a coin to decide which pair of shoes to wear: Heads or Tails

Roll a dice to decide which pair of pants to wear: 1 to 6 for each pair

Get a 8 sided dice/spinner with 8 segments/or flip 3 coins where each outcome corresponds with a shirt

Note: when you flip 3 coins, there are 8 outcomes:

ACTIVITY: IF YOU FLIP A COIN 100 TIMES, HOW MANY HEADSWILL YOU GET?

Theoretical Probability:

Experimental Probability:

Multiply that by 100 trialsto get the number of heads

Experimentally there could beanything from zero to 100 heads

If we did this activity, 0 or 100will be very unlikely, althoughit is still possible

The probability from asingle trial is 50%

So theoretically speaking,

in 100 trials, we should

expect to get 50 heads

Results from experimentalprobability would have to comefrom performing the experiment

One of the goals of mathematicians is to usetheoretical probability to predict the outcomes ofexperimental probability

When we play a game from rolling a dice, spinning aspinner, or flipping a coin, there’s a chance that we canwin or lose

We can use theoretical probability to calculate thatchance of winning or losing

In this lesson, we will learn to calculate how much wecan expect to win or lose when we play a game manynumber of times

“Expected Value” is amount that we can expect towin/lose in each game if we play it many number oftimes

I) EXPECTED VALUE

ACTIVITY: DICE GAME

Suppose it cost $1 to roll a die once and the payoff for eachoutcome is as follow:

Roll a die 20 times and record each outcome. Calculate yourpayoff after 20 rolls. Is this game worth playing?

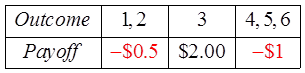
The probability distribution for this game is:

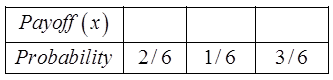
The expected value (long run pay off average) is:

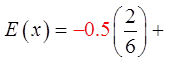
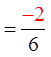
In the long run, you will lose 33.333 cents per game

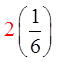
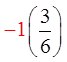
EX: GIVEN THE FOLLOWING SPINNER AND ITS PAYOFF,CALCULATE THE EXPECTED VALUE AND PAYOFF AFTER 20 SPINS:

Spin Button

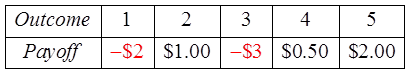
Note: Outcomes “4” and “5” are halfas likely to occur as the other numbers

Outcomes “1”, “2”, and “3” are 25%,

outcomes “4” and “5” are 12.5%

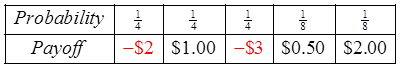
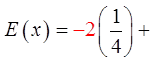
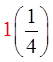
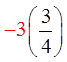
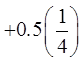
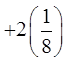
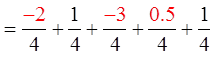
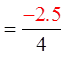
You can expect to lose62.5 cents each game.

In 20 games, youwill lose $12.50

HOMEWORK:

Handout