
SECTION 6.2SAMPLE SPACES FORINDEPENDENT EVENTS

WHAT ARE INDEPENDENT EVENTS?
Two events are considered “independent” if they do notaffect each other
For instance, what you eat for dinner tonight will notaffect the weather tomorrow two independent events
In mathematics, when we flip a coin, the outcome ofeach flip is independent of the one before/after it
Likewise, when we roll a die (dice) or spin a spinner,each roll/spin is independent
Note: if a dice favors one side more than others, thenthat dice is considered as “bias”

PRACTICE: GIVEN EACH PAIR OF EVENTS BELOW,INDICATE WHETHER IF THEY ARE INDEPENDENT OR NOT:
a) Flipping a coin and rolling a die
b) Drawing a card from a deck, keep it, and then draw thenext card. Will the first draw affect the second draw?
c) Flipping a coin 6 times. The first 5 times were heads.Will this affect the outcome of the 6th flip?
d) A basketball player shooting a free throw. Is each freethrow independent?
Each flip is independent!
Not independent because keeping the 1st card will affect theoutcome of the second draw
Independent b/c the outcomes of the first 5 flips do not affectthe next one
This one is arguably not independent b/c if the player missesthe first shot, he will naturally adjust to improve his next shot

SAMPLE SPACE WITH 2 OR MORE EVENTS
A sample space is a list of all the possible outcomes
When finding the sample space, draw a tree diagramto illustrate each outcome
Ex: A Spinner and die is rolled. If the spinner hits aneven number then the die is rolled. If odd, spinagain. Draw a sample space for this experiment:
Spinner
Even: 2,4
Odd: 1,3
1
2
3
4
5
6
1
2
3
4
The samplespace of thisexperiment is:
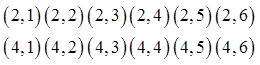
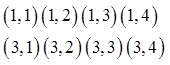

Practice: Given each event, find the sample space bydrawing a tree diagram:
a) A coin is tossed 3 times
b) One president and one captain is to be selected from agroup of 4 people: Amy, Brad, Chris, and Don
1st Coin
Heads
Tails
Heads
Tails
Heads
Tails
H
T
H
T
H
T
H
T
The samplespace is:
A
B
C
D
B
C
D
A
C
D
A
B
D
A
B
C
The first person will be the president
The second will be the captain
Your sample space will be:

THE FUNDAMENTAL COUNTING PRINCIPLE
One way to count the number of outcomes is by using the“Fundamental Counting Principle”
If we have “x” number of ways to do the first task and “y”number of ways to do the second task, then there are “x” times“y” ways to do both tasks.
If there are several different tasks:
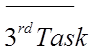
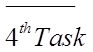
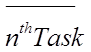

“A” – Number of ways to do the first task
“B” – Number of ways to do the second task
“C” – Number of ways to do the third task.... and so on
The total number of different ways to do all the task together will be:
© Copyright all rights reserved to Homework depot: www.BCMath.ca


EX: HOW MANY DIFFERENT 3 COURSE MEALS CAN YOU ORDER ATTHE SALMON HOUSE IF THERE ARE 3 DIFFERENT APPETIZERS, 4MAIN COURSE, AND 3 DIFFERENT DESSERTS.




There are three different categories:Appetizers, Mains, and Desserts
Use the Fundamental CountingPrinciples to count how many different
meals are possible
Multiply the number of choices in eachcategory
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: HOW MANY COMBINATIONS CAN YOU MAKE IFTHERE ARE 10 DIFFERENT ICINGS, 16 DIFFERENTICE-CREAMS, AND 10 DIFFERENT CONES.
FCP: Multiply the number of choices for eachcategory
© Copyright all rights reserved to Homework depot: www.BCMath.ca


EX: THE IPHONE HAS A 4 DIGIT NUMERICAL PASSWORD.WHAT IS THE TOTAL NUMBER OF DIFFERENT PASSWORDSTHAT ARE POSSIBLE.
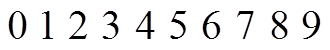
There are 10 choices from each digit:
1st method:
Count all the possibleoutcomes from thesmallest to the largestnumber
There are 10 thousanddifferent numbers possible
Multiply the number ofoptions for each digit
2nd method:
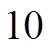
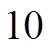
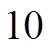
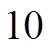
In total, there are:

© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:
P424 #4 to 16