
SECT 5.4 PROVINGTRIGONOMETRIC IDENTITIES
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PROVING IDENTITIES ALGEBRAICALLY:
When proving trigonometric identities:
Convert all trig. functions to sine or cosine
Use basic trig. Identities to simplify complicated ones
Odd/Even, Quotient, Pythagorean Identities
Start with the side that looks “more complicated”
You may need to rationalize the expression, factor outcommon factors, or multiply all terms by the LCD
Trial and Error (Do whatever it takes)
Once the left side and right side are equal then theequation is a trigonometric identity
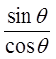
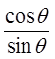
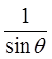
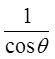
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PROVING TRIGONOMETRIC IDENTITIES BY USING BASICIDENTITIES:
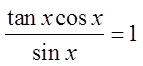
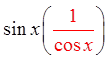
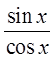
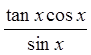
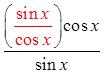
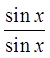
Quotient Identity!
Since the left side looks morecomplicated, we will prove theidentity from the left
Cancel out commonfactors
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PROVING BY ADDING/SUBTRACTING IDENTITIES
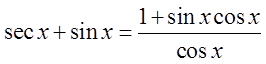
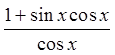
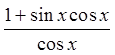
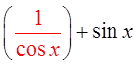
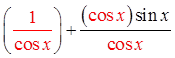
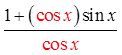
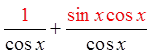
The proof may be the different
but the result is the same
You can also prove the identityfrom the other side
CommonDenominator
Combine the
Fractions
Split into 2separatefractions
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PRACTICE: PROVE THE FOLLOWING IDENTITIES:
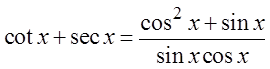
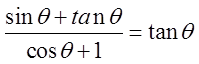
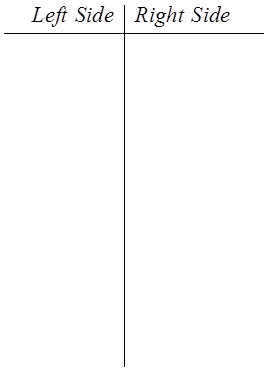
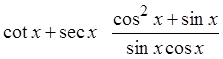
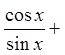
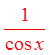
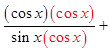
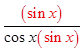
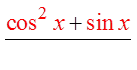
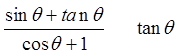

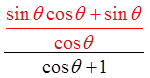
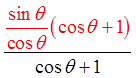
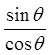
Factor out sin θ
CommonDenominator
Combine the
Fractions
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Get the LCD withthe numerator
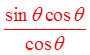

PROVING IDENTITIES USING FRACTIONS :
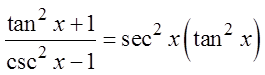
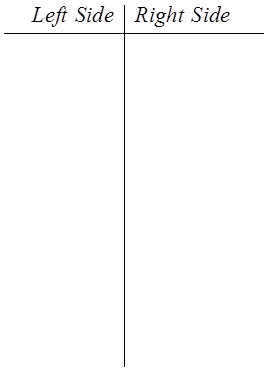
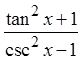
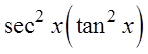
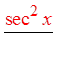
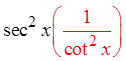
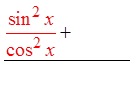
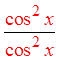
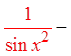
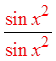
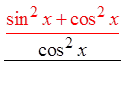
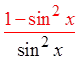
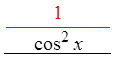
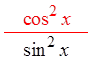
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Pythagorean
Identities
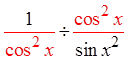
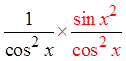
Divide thefractions

PROVING IDENTITIES BY FACTORING:
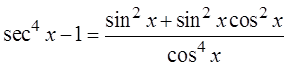
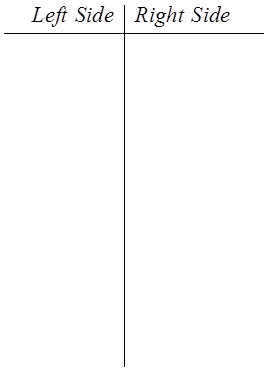
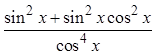
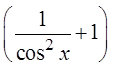
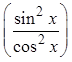
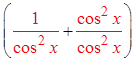
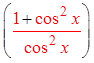
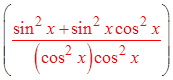
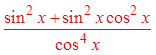
Difference ofsquares
Pythagoreanidentity
CommonDenominator
Expand
Factor out thesine function
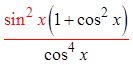
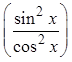
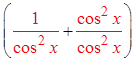
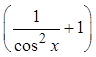
© Copyright all rights reserved to Homework depot: www.BCMath.ca
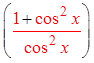
PythagoreanIdentity
FOIL

PRACTICE: PROVE THE FOLLOWING IDENTITIES BY FACTORING
Bracket thelast 2 terms
Pythagoreanidentity
Factor: Difference
of squares
PythagoreanIdentity
Factor theTrinomial
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PROVE BY CONJUGATING THE EXPRESSION:
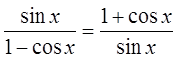
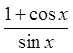


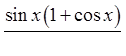
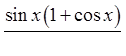
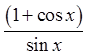
Multiply both top &bottom by the conjugate
Pythagoreanidentity
Expand
Quotient Identities
Reciprocal Identity
Pythagorean Identity
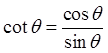
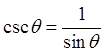
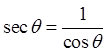
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Formula Sheet

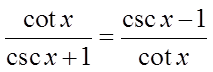
PRACTICE: PROVE THE FOLLOWING IDENTITY BY CONJUGATINGTHE EXPRESSION:
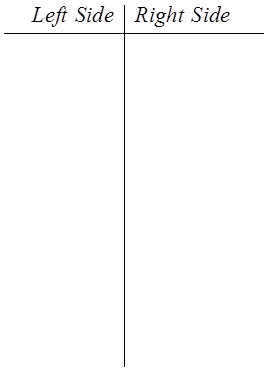
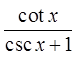
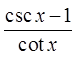
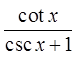
Multiply both top &bottom by the conjugate
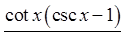
Expand
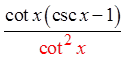
Pythagoreanidentity
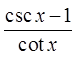
Quotient Identities
Reciprocal Identity
Pythagorean Identity
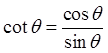
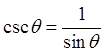
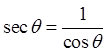
© Copyright all rights reserved to Homework depot: www.BCMath.ca
Formula Sheet
CLOSE
